A first order reaction is 50% completed in 20 minutes at 27∘ C and in 5 minutes at 47∘ . The energy of activation of the reaction is :
a) 43.85 KJ/mol
b) 55.14 KJ/mol
c) 11.97 KJ/mol
d) 6.65 KJ/molSolution in Punjabi
43.85 KJ/mol
55.14 KJ/mol
11.97 KJ/mol
6.65 KJ/mol
The correct Answer is:B
Step by step video & image solution for A first order reaction is 50% completed in 20 minutes at 27^(@) C and in 5 minutes at 47^(@) . The energy of activation of the reaction is : a) 43.85 KJ/mol b) 55.14 KJ/mol c) 11.97 KJ/mol d) 6.65 KJ/mol by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.93 To Q.122)19videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.123 To Q.150)10videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -21videos
SURFACE CHEMISTRY
Similar Questions
In the radioactive decay
.zXA→Z+1YA→Z−1ZA−4→Z−1ZA−4 high energy low energy the sequence of the radiation emitted is :03:34View SolutionActivity of a radioactive substance is A1 at time t1 and A2 at time t2(t2>t1) , then the ratio of fA2A1 is:
a) eλ(t2+t1)
b) eλ(t1−t2)
c) e−λ(t1+t2)
d) t2t105:48View Solutioncolumn Icolumn IIP.Zero order reaction1.t1/2α1[A]0Q.First order reaction2.t100%=[A]0/kR.second order reactions3.Involves at least two reactantsS.Pseudo unimolecular reaction4.[A]=[A]0e−kt
02:27View Solutionfor the graph below, select correct order of temperture ?
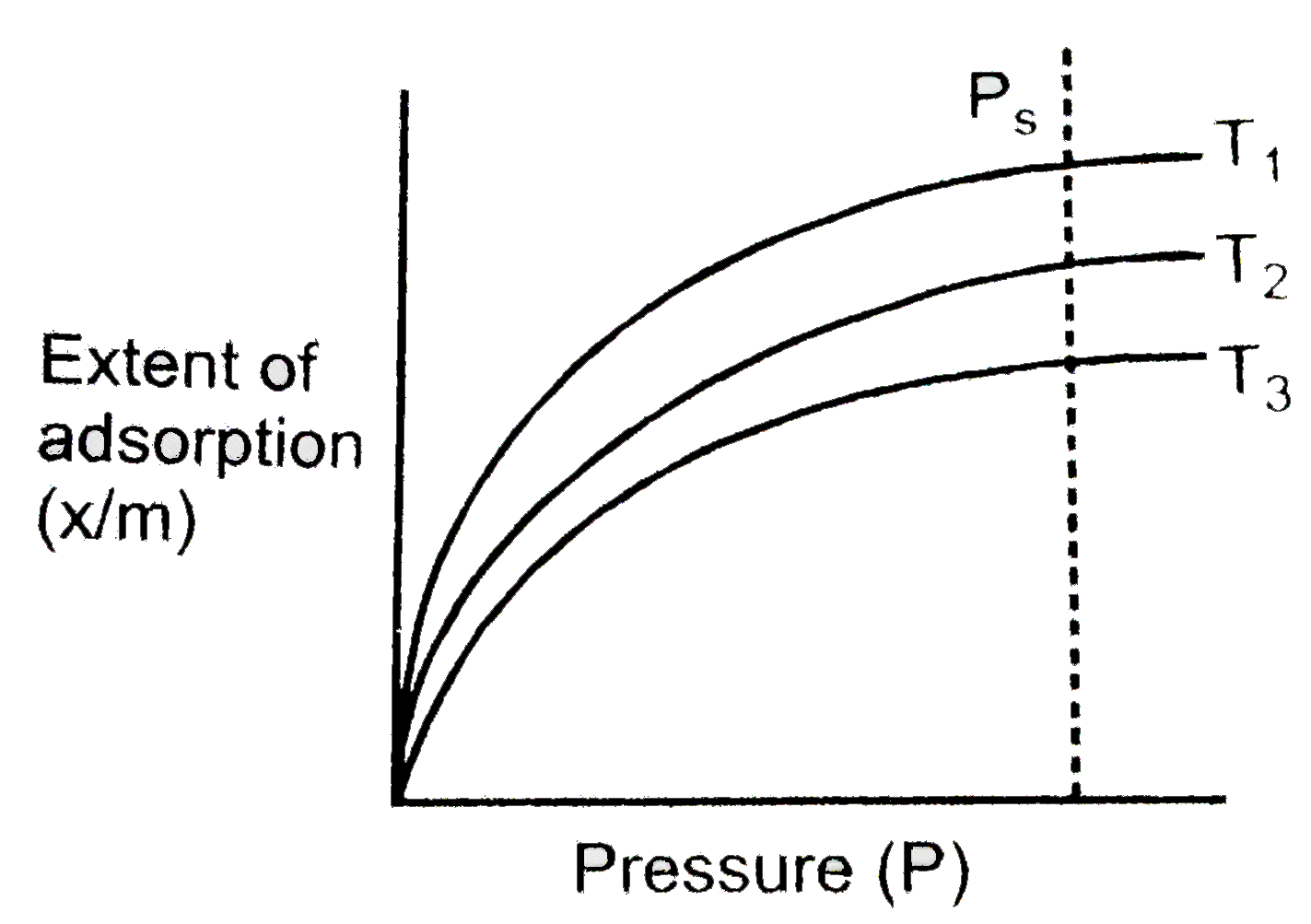 View Solution
View SolutionA first order reaction is 50% completed in 30 min at 27^(@)C and in 10 min at 47^(@)C . Calculate the reaction rate constants at 27^(@)C and the energy of activation of the reaction in kJ mol^(-1) .
View SolutionA 1st order reaction is 50% complete in 30 minute at 27^(@)C and in 10 minute at 47^(@)C . Calculate the: (a) Rate constant for reaction at 27^(@)C and 47^(@)C . (b) Energy of activation for the reaction. (c ) Energy of activation for the reverse reaction if heat of reaction is -50 kJ mol^(-1) .
06:11View SolutionFor A+B→C+D,ΔH=−20kJmol−1, the activation energy of the forward reaction is 85kJmol−1. The activation energy for backward reaction is …… kJmol−1.
View SolutionA first order reaction is 50% complete in 30 minutes at 27∘C and in 10 minutes at 47∘C. The rate constant at 47∘C and energy of activation of the reaction in kJ/mole will be
View SolutionA first order reaction is 50% complete in 30 minutes at 27^(@)C and in 10 minutes at 47^(@)C . The rate constant at 47^(@)C and energy of activation of the reaction in kJ // mole will be
05:46View SolutionA first order reaction is 50% complete in 30 minutes at 27^(@) C and in 10 minutes at 47^(@) C. Calculate the reaction rate constants at these temperatures and the energy of activation of the reaction in kJ//mol (R=8.314 J mol^(-1)K^(-1))
01:48View SolutionIf a reaction A+B→C is exothermic to the extent of 30 kJ/mol and the forward reaction has an activation energy of 70 kJ/mol, the activation energy for the reverse reaction is
01:48View SolutionA first order reaction in 50% completed in 30 minutes at 27^@C and in 10 minutes at 47^@C . Calculate the reaction rate constant at 27^@C and the energy of activation of eh reaction in kJ mol^(-1)
02:14View SolutionA first order reaction is 50% completed in 30min at 27∘C and in 10min at 47∘C. Calculate the reaction rate constants at 27∘C and the energy of activation of the reaction in kJmol−1.
02:38View SolutionFor A+B rarr C+D,DeltaH=-20 kJ mol^-1 , The activation energy of the forward reaction is 85 kJ mol^-1 . The activation energy for backward reaction is…….kJ mol^-1 :
01:44View SolutionFor A+B rarr C+D,DeltaH=-20 kJ mol^-1 , The activation energy of the forward reaction is 85 kJ mol^-1 . The activation energy for backward reaction is…….kJ mol^-1 :
05:38View Solution

