A He atom at 300 K is released from the surface of the earth to travel upwards. Assuming that it undergoes no collision with other molecules, how high will it be before coming to the rest?
9.53 m
9.5 m
953 m
9.53×104 m
The correct Answer is:d
To solve the problem of how high a helium atom will rise before coming to rest when released from the surface of the Earth, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy of the helium atom is conserved. Initially, it has kinetic energy (KE) when released, and as it rises, this kinetic energy is converted into gravitational potential energy (PE) until it comes to rest at its maximum height.
Step 2: Write the Equations for Kinetic and Potential Energy
The kinetic energy (KE) of the helium atom can be expressed as:
KE=32kBT
Where:
- kB is the Boltzmann constant (1.38×10−23J/K)
- T is the temperature in Kelvin (300 K)
The potential energy (PE) at height h is given by:
PE=mgh
Where:
- m is the mass of the helium atom
- g is the acceleration due to gravity (approximately 10m/s2)
- h is the height
Step 3: Calculate the Mass of the Helium Atom
The mass of a helium atom is approximately 4×1.67×10−27kg (since helium has 4 nucleons: 2 protons and 2 neutrons).
m=4×1.67×10−27=6.68×10−27kg
Step 4: Set Kinetic Energy Equal to Potential Energy
At the maximum height, all kinetic energy will have been converted to potential energy:
32kBT=mgh
Step 5: Substitute Known Values
Substituting the known values into the equation:
32(1.38×10−23)(300)=(6.68×10−27)(10)h
Step 6: Solve for Height h
First, calculate the left side:
32(1.38×10−23)(300)=6.21×10−21J
Now, substitute this into the equation:
6.21×10−21=(6.68×10−27)(10)h
6.21×10−21=6.68×10−26h
Now, solve for h:
h=6.21×10−216.68×10−26
h≈9.31×104m
Final Answer
The height h that the helium atom will reach before coming to rest is approximately:
h≈9.31×104meters
---
The total mechanical energy of the helium atom is conserved. Initially, it has kinetic energy (KE) when released, and as it rises, this kinetic energy is converted into gravitational potential energy (PE) until it comes to rest at its maximum height.
The kinetic energy (KE) of the helium atom can be expressed as:
KE=32kBT
Where:
- kB is the Boltzmann constant (1.38×10−23J/K)
- T is the temperature in Kelvin (300 K)
PE=mgh
Where:
- m is the mass of the helium atom
- g is the acceleration due to gravity (approximately 10m/s2)
- h is the height
The mass of a helium atom is approximately 4×1.67×10−27kg (since helium has 4 nucleons: 2 protons and 2 neutrons).
m=4×1.67×10−27=6.68×10−27kg
At the maximum height, all kinetic energy will have been converted to potential energy:
32kBT=mgh
Substituting the known values into the equation:
32(1.38×10−23)(300)=(6.68×10−27)(10)h
First, calculate the left side:
32(1.38×10−23)(300)=6.21×10−21J
6.21×10−21=(6.68×10−27)(10)h
6.21×10−21=6.68×10−26h
h=6.21×10−216.68×10−26
h≈9.31×104m
The height h that the helium atom will reach before coming to rest is approximately:
h≈9.31×104meters
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 230videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
If nitrogen gas molecule goes straight up with its rms speed at 0∘C from the surface of the earth and there are no collisions with other molecules, then it will rise to an approximate height of.
View SolutionA gas molecule at the surface of earth happens to have the rms speed for the gas at 0∘C . Suppose it went straight up without colliding with other molecules, how high it would rise? Mass of the molecule is 4.65×10−26kg. Boltzmann's constant =1.38×10−23JK−1.
View Solution
Knowledge Check
- Question 1 - Select One
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
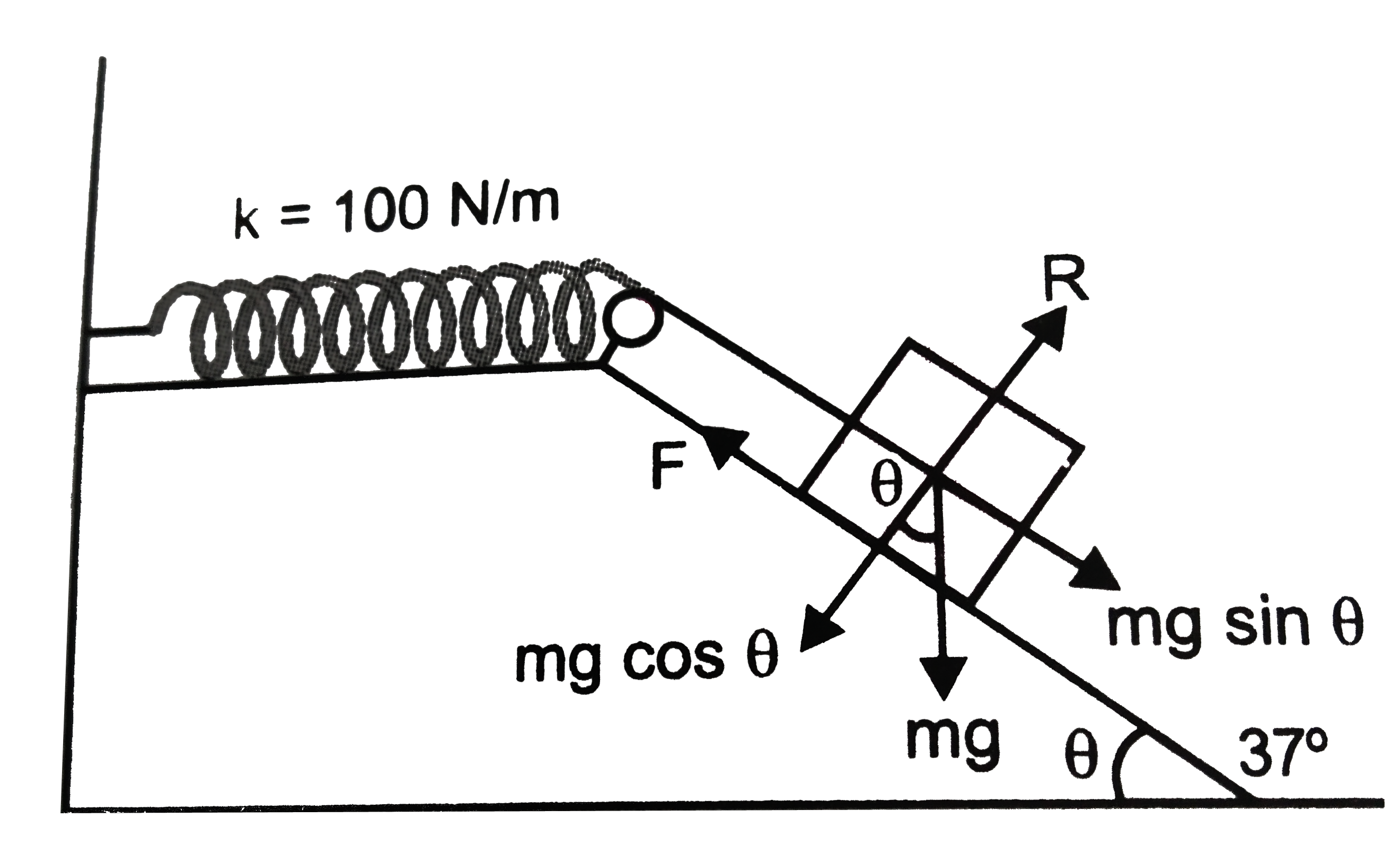A0.2B0.3C0.5D0.6
A particle is given a velocity ve√3 in a vertically upward direction from the surface of the earth, where ve is the escape velocity from the surface of the earth. Let the radius of the earth be R. The height of the particle above the surface of the earth at the instant it comes to rest is :
View SolutionThe speed of a train is reduced from 60 km/h, to 15 km/h, while it travels a distance of 450 m. If the retardation is uniform, find how much further it will travel before coming to rest ?
View SolutionTwo balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution_E01_050_Q01.png)
A small ball of mass 'm' is released at a height 'R' above the earth surface, as shown in the figure. If the maximum depth of the ball to which it goes is R/2 inside the earth through a narrow grove before coming to rest momentarily. the grove, contain an ideal spring of spring constant K and natural length R, the value of K is (R is radius of Earth and M mass of Earth)View SolutionThe block shown in the figure is acted on by a sping with spring constant (k) and (a) weak frictional force of constant of constant magitude (f.) The block is pulled a distance x0 from equilibrium position and then then then fren released. It oscillates many times ultimately comes to rest.
(a) Show that the decrease of amplitude is the same for each cycle of lscillation.
(b) Find the number of cycles the mass oscillates before coming to rest.View SolutionA 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
View Solution