A piece of mass 36.81 kg is cut from a block of 4.0×102 kg. Calculate the mass of the remaining block upto proper significant figures.
To solve the problem of calculating the mass of the remaining block after cutting a piece from it, we can follow these steps:
Step 1: Identify the given masses
- Total mass of the block = 4.0×102 kg
- Mass of the piece cut from the block = 36.81 kg
Step 2: Convert the total mass into a standard form
- The total mass can be expressed as:
4.0×102 kg=400 kg
Step 3: Subtract the mass of the cut piece from the total mass
- To find the mass of the remaining block, we perform the subtraction:
Remaining mass=Total mass−Mass of the piece cut
Remaining mass=400 kg−36.81 kg=363.19 kg
Step 4: Determine the significant figures
- The total mass (400 kg) has 2 significant figures (the "4" and the "0" after the decimal).
- The mass of the piece cut (36.81 kg) has 4 significant figures.
Step 5: Apply the rules of significant figures for subtraction
- When performing subtraction, the result should be reported with the same number of decimal places as the measurement with the least number of decimal places.
- The total mass (400 kg) has no decimal places, while the mass of the piece cut (36.81 kg) has two decimal places. Therefore, we will round our answer based on the total mass.
Step 6: Round the result to the appropriate significant figures
- The result of 363.19 kg must be rounded to 1 decimal place (because 400 kg has no decimal places).
- Rounding 363.19 kg to 1 decimal place gives us 363.2 kg.
Final Answer
The mass of the remaining block is:
Remaining mass=363.2 kg
---
- Total mass of the block = 4.0×102 kg
- Mass of the piece cut from the block = 36.81 kg
- The total mass can be expressed as:
4.0×102 kg=400 kg
- To find the mass of the remaining block, we perform the subtraction:
Remaining mass=Total mass−Mass of the piece cut
Remaining mass=400 kg−36.81 kg=363.19 kg
- The total mass (400 kg) has 2 significant figures (the "4" and the "0" after the decimal).
- The mass of the piece cut (36.81 kg) has 4 significant figures.
- When performing subtraction, the result should be reported with the same number of decimal places as the measurement with the least number of decimal places.
- The total mass (400 kg) has no decimal places, while the mass of the piece cut (36.81 kg) has two decimal places. Therefore, we will round our answer based on the total mass.
- The result of 363.19 kg must be rounded to 1 decimal place (because 400 kg has no decimal places).
- Rounding 363.19 kg to 1 decimal place gives us 363.2 kg.
The mass of the remaining block is:
Remaining mass=363.2 kg
Topper's Solved these Questions
- SOME BASIC CONCEPTS OF CHEMISTRY BOOK - ICSECHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - REVIEW EXERCISES
129 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY BOOK - ICSECHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
34 Videos
- SELF ASSESSMENT PAPER 2BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 2EXERCISE - Questions
62 Videos
- SOME P-BLOCK ELEMENTS BOOK - ICSECHAPTER - SOME P-BLOCK ELEMENTS EXERCISE - NCERT TEXTBOOK EXERCISES (With Hints and Solutions)
63 Videos
Similar Questions
Knowledge Check
A trolley of mass 20 kg is attached to a block of mass 4kg by massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the accderal ion of the trolley and block system is (Takeg=10ms−2)
 A1ms−2B2ms−2C1.5ms−2D2.5ms−2
A1ms−2B2ms−2C1.5ms−2D2.5ms−2
In the figure shown the man of mass 60kg is lowering a block of mass 10kg with an acceleration of 2m/s2. Find the reading of the machine.

View Solution
Block B of mass 2 kg rests on block A of mass 10 kg. All surfaces are rough with the value of coefficient of friction as shown in the figure. Find the minimum force F that should ber appplied on blocks A to cause relative motion between A and B.(g=10ms2)
View Solution
Block B of mass 2 kg rests on block A of mass 10 kg. All surfaces are rough with the value of coefficient of friction as shown in the figure. Find the minimum force F that should ber appplied on blocks A to cause relative motion between A and B.(g=10ms2)
View SolutionBlock B of mass 2kg rests on block A of mass 10kg. All surfaces are rought with the value of coefficient of friction as shown in the figure. Find the minimum force F that should be applied on block A to cause relative motion between A and B. (g=10m/s2)

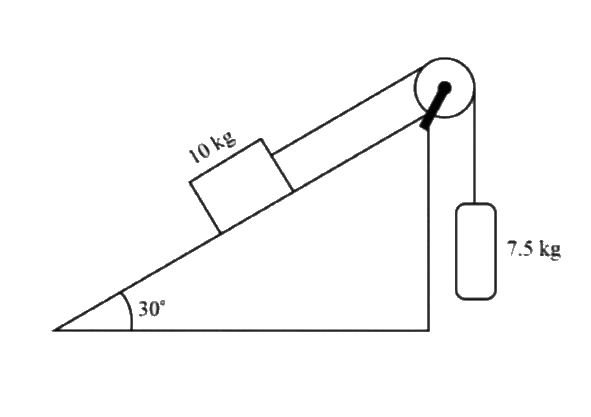
View SolutionAll surfaces shown in the figure are frictionless. A block of mass 2 kg is kept on a wedge of mass 10 kg. If the mass m remains stationary w.r.t wedge , the magnitude of force P is ( g = 10m/s2)
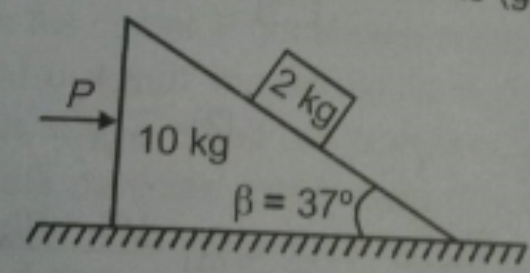
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
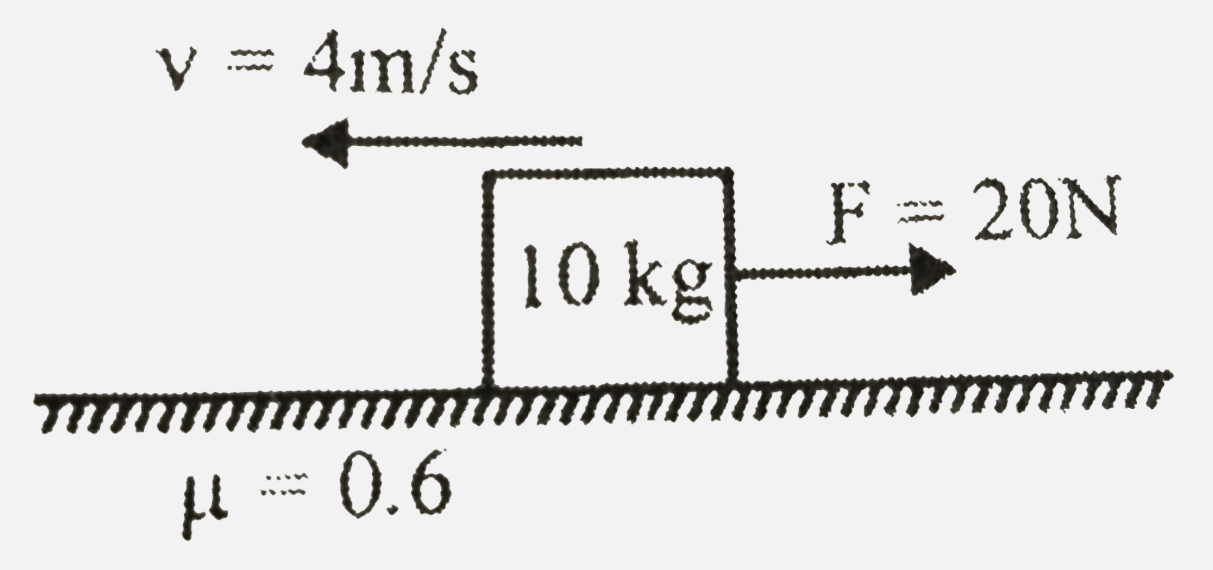
View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
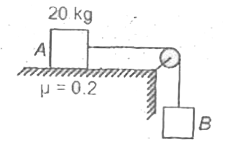
View Solution