A radioactive isotopeA undergoes simultaneous decay to two different nuclei as
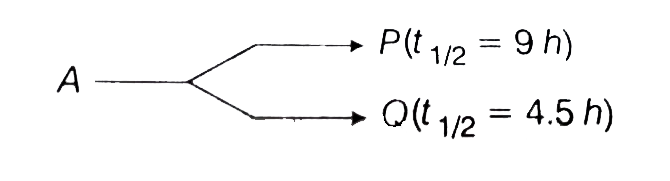
Assuming that initially neither P norQ was present, after how many hours, amount of Q will be just double to the amount of A remaining?
Both Assertion and Reason are correct and Reason is the correct explanation of the Assertion
Both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
Assertion is correct but Reason is incorrect
Assertion is incorrect but Reason is correct
The correct Answer is:6
Topper's Solved these Questions
Similar Questions
A radioactive material is undergoing simultaneous disintegration into two different products with half lives 1400 years and 700 years respectively.Find the time taken by the sample to decay to one third of its initial value .
View SolutionA radioactive sample decays through two different decay processes α-decay and β-decay is 6h. What will be the ratio of number of radioactive nuclei present after 6h?.
View Solution
Knowledge Check
A radioactive element undergoing decay is left 20% of its initial weight after certain period of time t. How many such periods should elapse from the start for the 50% of the element to be left over?
A3B4C5Dnone of theseA sample of radioactive material decays simultaneouly by two processes A and B with half-lives 12 and 14h, respectively. For the first half hour it decays with the process A, next one hour with the proecess B, and for further half an hour with both A and B. If, origianlly, there were N0 nuceli, find the number of nuclei after 2 h of such decay.
AN0(2)8BN0(2)4CN0(2)6DN0(2)5A radioactive isotope decays at such a rate that after 192 minutes only 1/16 of the original amount remains. The half life of the radioactive isotope is
A32 minB48 minC12 minD24 min
A certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View SolutionA certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View SolutionA certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View SolutionA radioactive isotope decays at such a rate that after 192 minutes only 1/16 of the original amount remains. The half life of the radioactive isotope is
View SolutionA radioactive isotope decays to such a rate that after 96 min only 1/8th of the original amount remains. The value t1/2 of this nuclide is
View Solution
