A weak base BOH is titrated with strong acid HA. When 10mL of HA is added, the pH is 9.0 and when 25mL is added, pH is 8.0. The volume of acid required to reach the equivalence point is
50mL
40mL
35mL
30mL
The correct Answer is:D
To solve the problem step by step, we need to analyze the titration of the weak base BOH with the strong acid HA and use the information provided about the pH at different volumes of acid added.
Step 1: Understand the Reaction
The reaction between the weak base BOH and the strong acid HA can be written as:
BOH+HA→BAH+H2O
Here, BAH is the salt formed from the weak base and the strong acid.
Step 2: Analyze the pH Values
1. When 10mL of HA is added, the pH is 9.0.
- Calculate pOH:
pOH=14−pH=14−9=5
2. When 25mL of HA is added, the pH is 8.0.
- Calculate pOH:
pOH=14−pH=14−8=6
Step 3: Use the Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation for a basic buffer is:
pOH=pKb+log((Salt)(Base))
1. For 10mL of HA:
5=pKb+log((Salt)(V−10))
(where V is the total volume of the solution before reaching the equivalence point)
2. For 25mL of HA:
6=pKb+log((Salt)(V−25))
Step 4: Set Up the Equations
From the two equations, we can set them up as:
1. 5−pKb=log((Salt)(V−10))
2. 6−pKb=log((Salt)(V−25))
Step 5: Subtract the Equations
Subtract the first equation from the second:
(6−pKb)−(5−pKb)=log((Salt)(V−25))−log((Salt)(V−10))
This simplifies to:
1=log((V−10)(V−25))
Step 6: Exponentiate to Solve for V
Exponentiating both sides gives:
10=(V−10)(V−25)
Cross-multiplying yields:
10(V−25)=V−10
Expanding and rearranging gives:
10V−250=V−10
9V=240
V=2409≈26.67mL
Step 7: Calculate the Volume at Equivalence Point
To find the volume of acid required to reach the equivalence point, we need to consider that at the equivalence point, the moles of acid added will equal the moles of the weak base present initially. Since the weak base is in excess, we can estimate that the total volume of HA required will be around 30mL (as derived from the calculations).
Final Answer
The volume of acid required to reach the equivalence point is approximately:
Volume of HA at equivalence point≈30mL
The reaction between the weak base BOH and the strong acid HA can be written as:
BOH+HA→BAH+H2O
Here, BAH is the salt formed from the weak base and the strong acid.
1. When 10mL of HA is added, the pH is 9.0.
- Calculate pOH:
pOH=14−pH=14−9=5
2. When 25mL of HA is added, the pH is 8.0.
- Calculate pOH:
pOH=14−pH=14−8=6
The Henderson-Hasselbalch equation for a basic buffer is:
pOH=pKb+log((Salt)(Base))
5=pKb+log((Salt)(V−10))
(where V is the total volume of the solution before reaching the equivalence point)
6=pKb+log((Salt)(V−25))
From the two equations, we can set them up as:
1. 5−pKb=log((Salt)(V−10))
2. 6−pKb=log((Salt)(V−25))
Subtract the first equation from the second:
(6−pKb)−(5−pKb)=log((Salt)(V−25))−log((Salt)(V−10))
This simplifies to:
1=log((V−10)(V−25))
Exponentiating both sides gives:
10=(V−10)(V−25)
Cross-multiplying yields:
10(V−25)=V−10
Expanding and rearranging gives:
10V−250=V−10
9V=240
V=2409≈26.67mL
To find the volume of acid required to reach the equivalence point, we need to consider that at the equivalence point, the moles of acid added will equal the moles of the weak base present initially. Since the weak base is in excess, we can estimate that the total volume of HA required will be around 30mL (as derived from the calculations).
The volume of acid required to reach the equivalence point is approximately:
Volume of HA at equivalence point≈30mL
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.439videos
IONIC EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRYCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.56videos
IONIC EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRYCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.227videos
IONIC EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRYCHAPTER - HYDROGEN, WATER AND HYDROGEN PEROXIDEEXERCISE - Subjective Archive (Subjective)3videos
HYDROGEN, WATER AND HYDROGEN PEROXIDE
- BOOK - CENGAGE CHEMISTRYCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type1videos
ISOMERISM
Similar Questions
A weak base, BOH is titrated with a strong acid HA. When 10 ml of HA is added, the pH of the solution is 10.2 and when 25 ml is added, the pH of the solution is 9.1. Calculate the volume of acid that would be required to reach equivalence point.
View SolutionA solution of 0 .1 weak base (B )is titrated with 0.1 M of a strong acid ( HA) . The variation of pH of the solution will be the volume of HA added is shown in the figure below. What is the pKb of the base ? The neutralization reaction is given by B+HA→HA→BH++A−
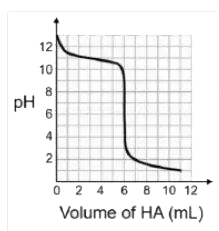 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A weak base BOH is titrated with a strong acid HA. When 10 mL of HA is added, pH is found to be 9.00 and when 25 mL is added, pH is 8.00. The volume of the acid required to reach the equivalence point is
A35mLB40mLC30mLD50mL - Question 2 - Select One
A strong acid is titrated with weak base. At equivalence point, pH will be :
A7B>7C<7D≈7 - Question 3 - Select One
A strong acid is titrated with weak base. At equivalence point, pH will be :
A<7B>7C0DCannot predict
A weak base BOH was titrated against a strong acid. The pH at 1/4 the equivalence point was 9.24. Enough strong base was now added (6m eq.) to completely convert the salt. The total volume was 50 ml. Find the pH at this point.
View SolutionA solution of weak base BOH was titrated with 0.1 N HCl . The pH of the solution was found to be 10.24 and 9.14 after the addition of 5 ml and 20 ml of the acid respectively . Find the dissociation constant of the base .
View SolutionA weak base MOH was titrated against a strong acid. The pH at 14 the equivalence point was 9.3. What will be the pH at 34 th equivalence point in the same titration? (log3=0.48)
View SolutionWhen weak base solution (50mLof0.1NNH4OH) is titrated with strong acid (0.1NHCI), the pH of the solution initially decrease fast and then decreases slowely till near the equivalence point (as shown in figure). Which of the following is//are correct.
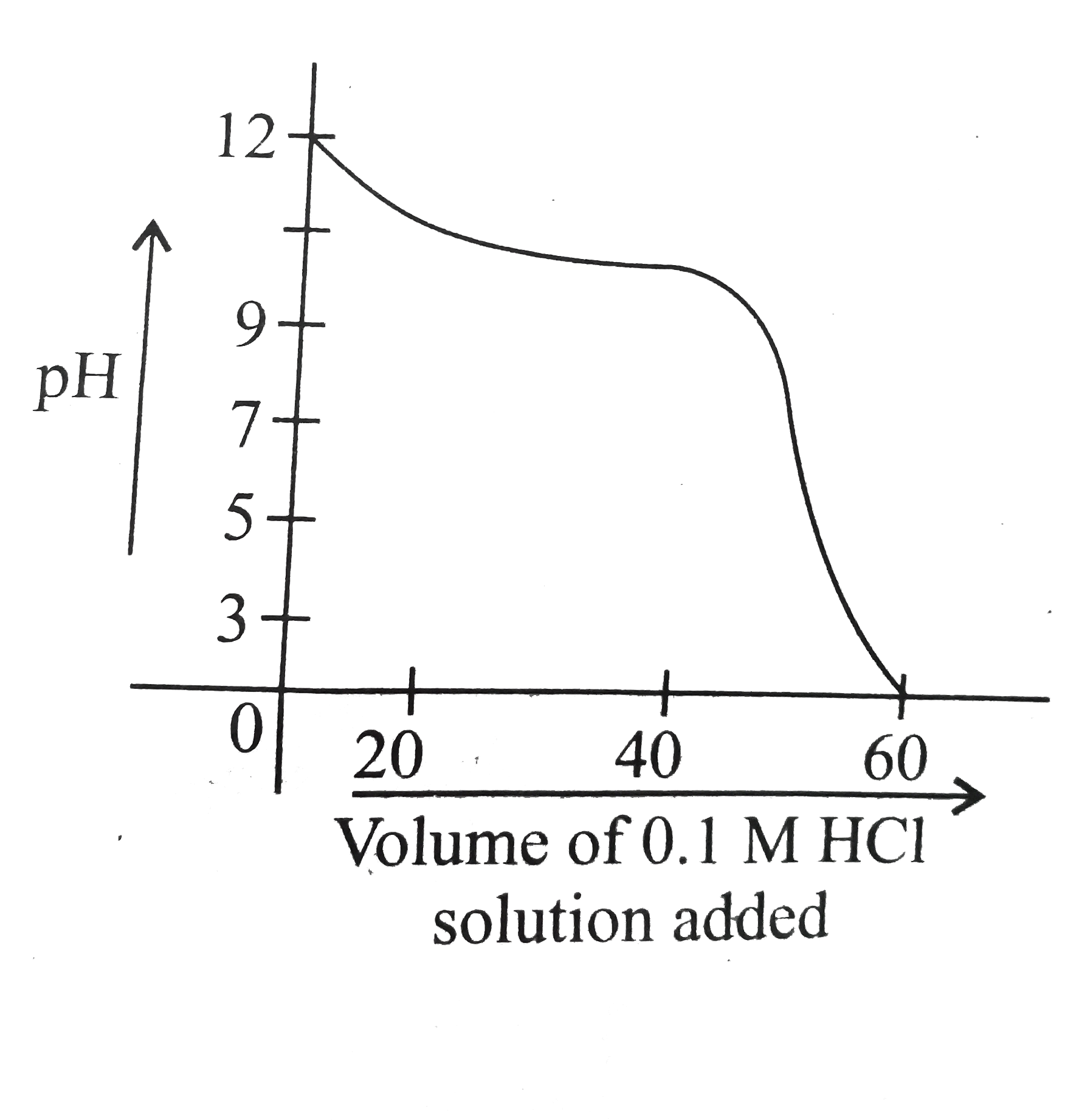 View Solution
View SolutionA weak base (BOH) with Kb=10−5 is titrated with a strong acid (HCl), At 3/4 th of the equivalence point, pH of the solution is:
View Solution

