A1 and A2 are two ores of metal M.A1 on calcination gives a black precipitate, CO2 and water. Identify A1 and A2.
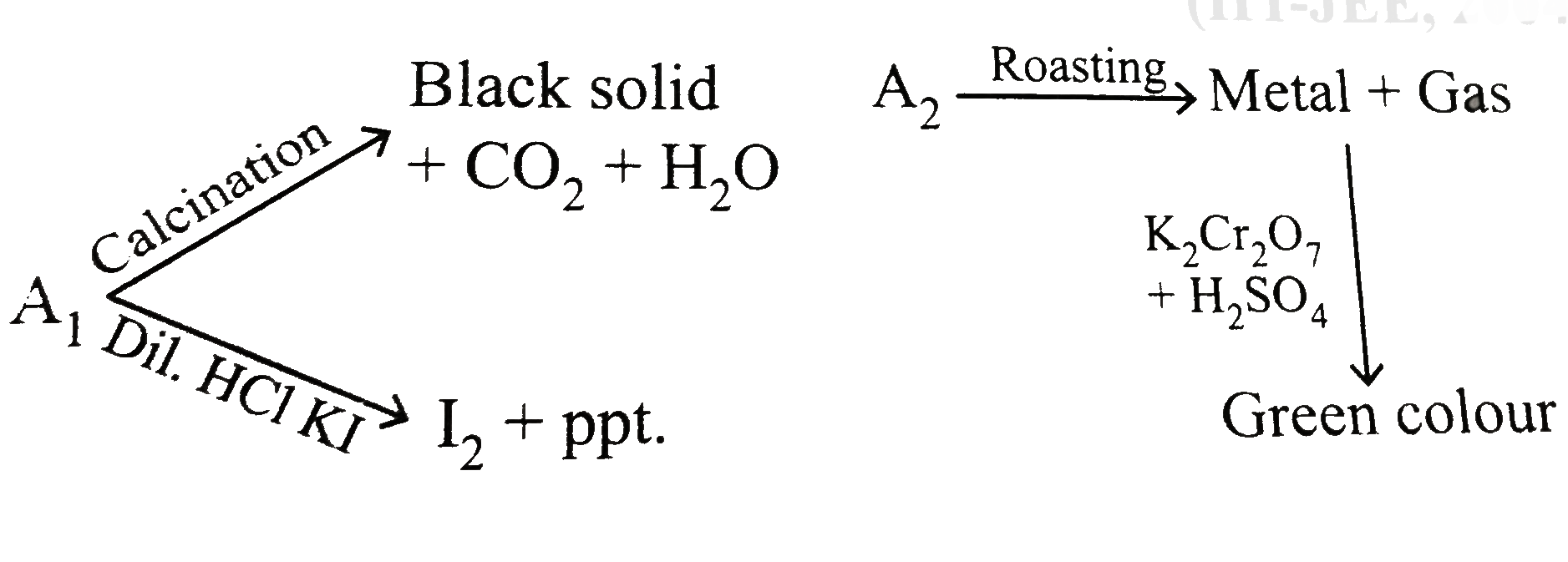 .
.
A1 is malachite CuCO3.Cu(OH)2
CuCO3.Cu(OH)2Δ−−→2CuO+CO2↑⏐⏐+H2O
CuO is the black solid.
CuCO3.Cu(OH)2Dil.HCl−−−−→CuCl2+CO2+H2O
CuCl2KI−−→Cu2I2+KCl+I2
A2 is copper glance, Cu2S, sulphide ore.
Cu2SO2.Δ−−−→Cu2O+SO2
Cu2S+Cu2O→Cu+SO2
The gas SO2 gives green colour with acidified K2Cr2O7.
K2Cr2O7+H2SO4+3SO2→K2SO4+Cr2Green(SO4)3+4H2O.
Topper's Solved these Questions
- GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSEXERCISE - Archives (Fill In The Blanks)
4 Videos
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Archieves Subjective
35 Videos
- GRIGNARD REAGENTS AND ORGANOMETALLIC REAGENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - GRIGNARD REAGENTS AND ORGANOMETALLIC REAGENTSEXERCISE - Exercises Archives (Linked Comprehension)
1 Videos
Similar Questions
A1&A2 are two ores of metal M. Ar on calcination gives black precipitate, CO2& water.

View SolutionLet points A1,A2andA3 lie on the parabola y2=8x. If △A1A2A3 is an equilateral triangle and normals at points A1,A2andA3 on this parabola meet at the point (h, 0). Then the value of h I s
View SolutionA1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
View SolutionIf a0,a1,a2,… are the coefficients in the expansion of
(1+x+x2)n in ascending powers of x, prove that
a0a2−a1a3+a2a4−…+a2n−2a2n=an+1 .
View SolutionIf →a1and→a2 are two non-collinear unit vectors and if ∣∣→a1+→a2∣∣=√3, then the value of (→a1−→a2).(2→a1+→a2) is :
View SolutionIf a1anda2 are two non- collinear unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionIf A1,A2 are between two numbers, then A1+A2H1+H2 is equal to
View Solutiona1,a2,a3∈R−{0}anda1+a2cos2x+a3sin2x=0 " for all " x in R then (a) vectors →a=a1ˆi+a2ˆj+a3ˆkand→b=4ˆi+2ˆj+ˆk are perpendicular to each other (b)vectors →a=a1ˆi+a2ˆj+a3ˆkand→b=ˆi+ˆj+2ˆk are parallel to each each other (c)if vector →a=a1ˆi+a2ˆj+a3ˆk is of length √6 units, then on of the ordered trippplet (a1,a2,a3)=(1,−1,−2) (d)if 2a1+3a2+6a3=26, then ∣∣→aˆi+a2ˆj+a3ˆk∣∣is2√6
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
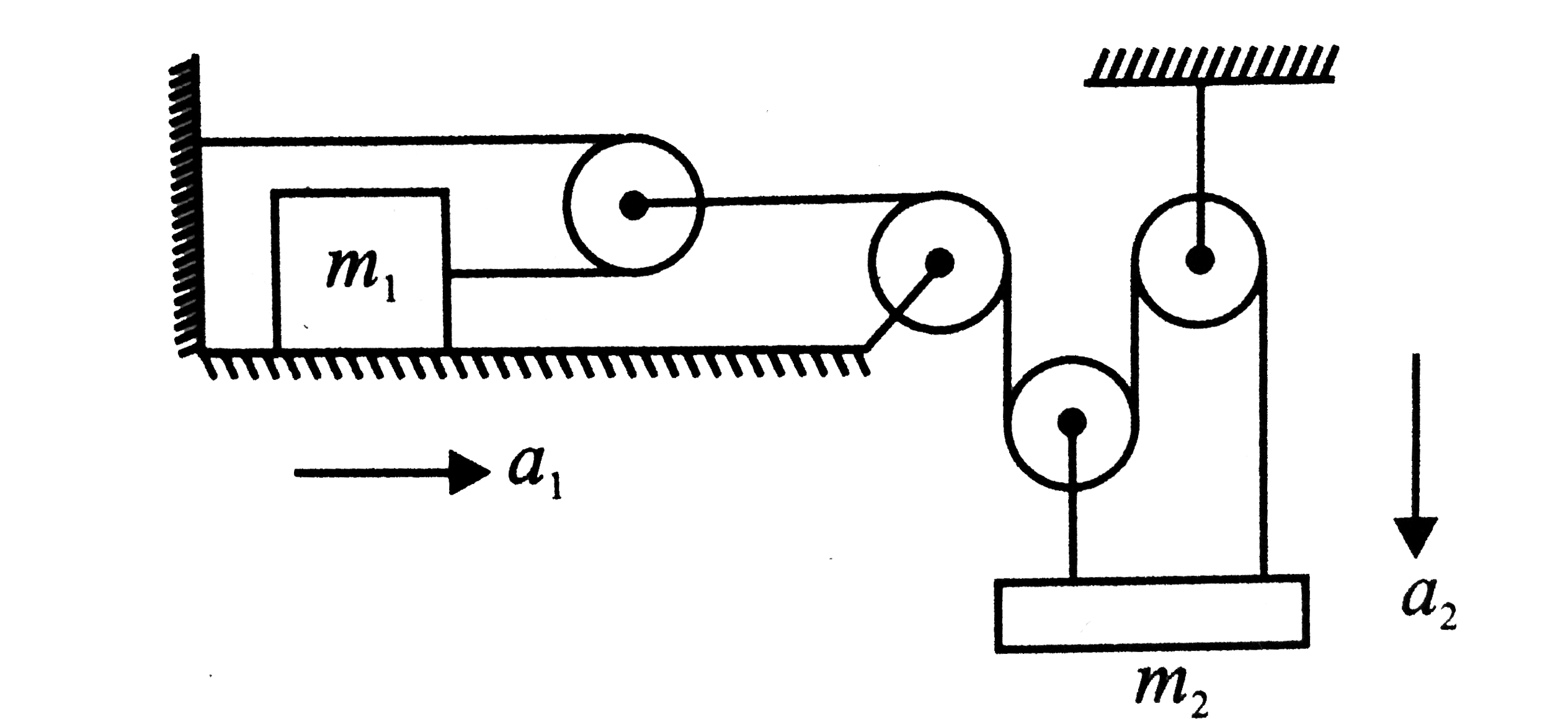
View Solution
