At room temperature, ammonia gas at 1 atm pressure and hydrogen chloride gas at P atm pressure are allowed to effuse through identical pin holes from opposite ends of a glass tube of one metre length and of uniform cross section. Ammonium chloride is first formed at a distance of 60 cm from the end through which HCl gas is sent in. What is the value of P?
The correct Answer is:2.198 atm
To solve the problem, we will use Graham's law of effusion, which states that the rate of effusion of a gas is inversely proportional to the square root of its molar mass. We will denote the rates of effusion for ammonia (NH₃) and hydrogen chloride (HCl) and set up the equation accordingly.
1. Identify the Given Information:
- Pressure of ammonia (NH₃), PNH₃=1atm
- Pressure of hydrogen chloride (HCl), PHCl=Patm
- Distance where ammonium chloride forms = 60 cm from HCl end
- Total length of the tube = 100 cm
2. Define the Rates of Effusion:
- Let RNH₃ be the rate of effusion of NH₃ and RHCl be the rate of effusion of HCl.
- From Graham's law, we have:
RNH₃RHCl=PNH₃PHCl⋅√MHClMNH₃
- Where MHCl=36.5g/mol and MNH₃=17g/mol.
3. Calculate the Distances Traveled:
- The distance traveled by NH₃ is 40cm (since it travels from the opposite end to where the reaction occurs).
- The distance traveled by HCl is 60cm.
4. Set Up the Ratios:
- The time taken for both gases to travel their respective distances is the same, so we can express the rates in terms of distance:
RNH₃=40tandRHCl=60t
- Substituting these into Graham's law gives:
40/t60/t=1P⋅√36.517
5. Simplify the Equation:
- The t cancels out:
4060=1P⋅√36.517
- Simplifying 4060 gives 23:
23=1P⋅√36.517
6. Calculate the Square Root:
- Calculate √36.517:
√36.517≈√2.147≈1.465
7. Substitute Back to Find P:
- Rearranging gives:
P=1.465⋅32=4.3952≈2.1975
8. Final Answer:
- Thus, the value of P is approximately 2.198atm.
- Pressure of ammonia (NH₃), PNH₃=1atm
- Pressure of hydrogen chloride (HCl), PHCl=Patm
- Distance where ammonium chloride forms = 60 cm from HCl end
- Total length of the tube = 100 cm
- Let RNH₃ be the rate of effusion of NH₃ and RHCl be the rate of effusion of HCl.
- From Graham's law, we have:
RNH₃RHCl=PNH₃PHCl⋅√MHClMNH₃
- Where MHCl=36.5g/mol and MNH₃=17g/mol.
- The distance traveled by NH₃ is 40cm (since it travels from the opposite end to where the reaction occurs).
- The distance traveled by HCl is 60cm.
- The time taken for both gases to travel their respective distances is the same, so we can express the rates in terms of distance:
RNH₃=40tandRHCl=60t
- Substituting these into Graham's law gives:
40/t60/t=1P⋅√36.517
- The t cancels out:
4060=1P⋅√36.517
- Simplifying 4060 gives 23:
23=1P⋅√36.517
- Calculate √36.517:
√36.517≈√2.147≈1.465
- Rearranging gives:
P=1.465⋅32=4.3952≈2.1975
- Thus, the value of P is approximately 2.198atm.
Topper's Solved these Questions
- STATES OF MATTER : GASES AND LIQUIDSBOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - NCERT TEXT-BOOK EXERCISES (With Hints and Solutions)
23 Videos
- STATES OF MATTER : GASES AND LIQUIDSBOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
5 Videos
- SOME P-BLOCK ELEMENTS BOOK - ICSECHAPTER - SOME P-BLOCK ELEMENTS EXERCISE - NCERT TEXTBOOK EXERCISES (With Hints and Solutions)
63 Videos
- STRUCTURE OF ATOMBOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - NCERT Textbook Exercises
67 Videos
Similar Questions
At room temperature, ammonia gas at 1atm pressure and hydrogen chloride gas at Patm pressure are allowed to effuse through identical pin holes from opposite ends of a glass tube of 1m length and of uniform cross- section. Ammonium chloride is first formed at a distance of 60cm from the end through which HCl gas is sent in. What is the value of P?
View SolutionThrough the two ends of a glass tube of length 200cm hydrogen chloride gas and ammonia are allowed to enter At what distance ammonium chloride will first appear ? .
View SolutionX and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.
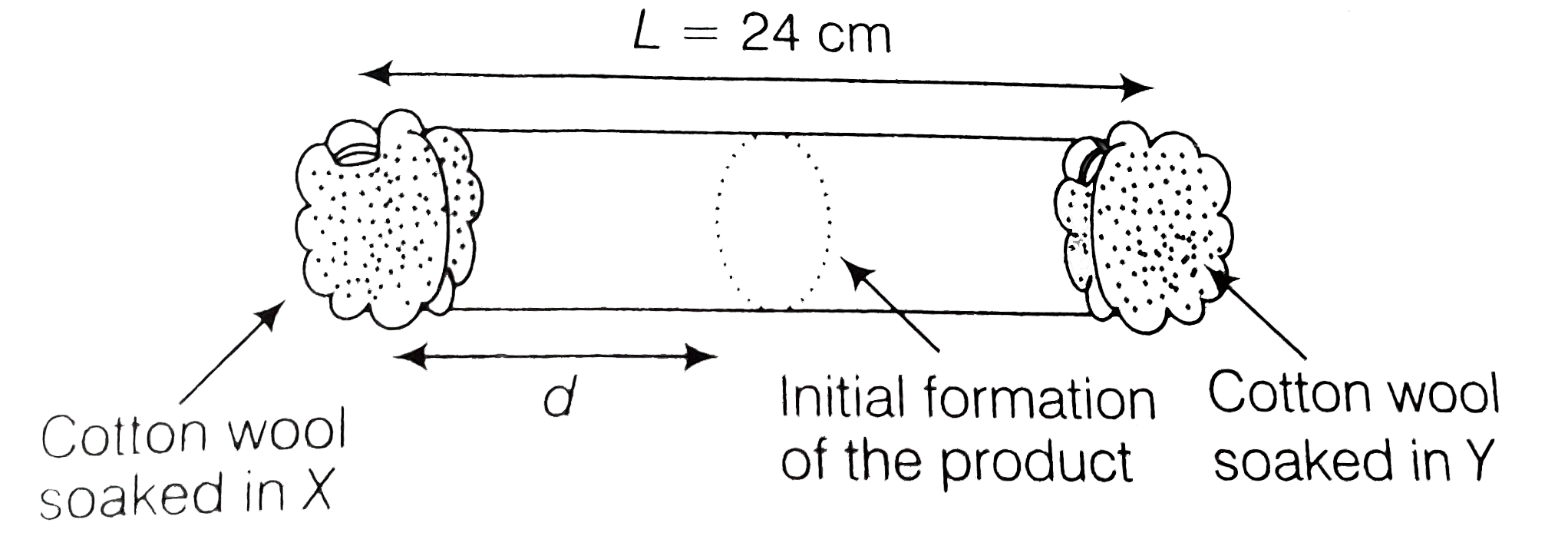
The value of d in cm (shown in figure), as estimated from Graham's law, is
View SolutionX and Y are two volatile liquids with molar weights of 10gmol−1 and 40gmol−1 respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube of length L=24 cm, as shown in the figure.
The tube is filled with an inert gas at 1 atm pressure and a temperature of 300K. Vapours of X and Y react to form a product whichh is first observed at a distance dcm from the plug soaked in X.
Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and two vapours.

The value of d in cm (shown in figure), as estimated from Graham's law, is
View SolutionAt 27∘C, hydrogen is leaked through a tiny hole into a vessel for 20min. Another unknown gas at the same temperature and pressure as that of hydrogen is leaked through the same hole for 20min. After the effusion of the gases, the mixture exerts a pressure of 6atm. The hydrogen content of the mixture is 0.7mol. If the volume of the container is 3L, what is the molecular weight of the unknown gas?
View SolutionAt 27∘C, hydrogen is leaked through a tiny hole into a vessel for 20min. Another unknown gas at the same temperature and pressure as that of hydrogen is leaked through the same hole for 20min. After the effusion of the gases, the mixture exerts a pressure of 6atm. The hydrogen content of the mixture is 0.7mol. If the volume of the container is 3L, what is the molecular weight of the unknown gas?
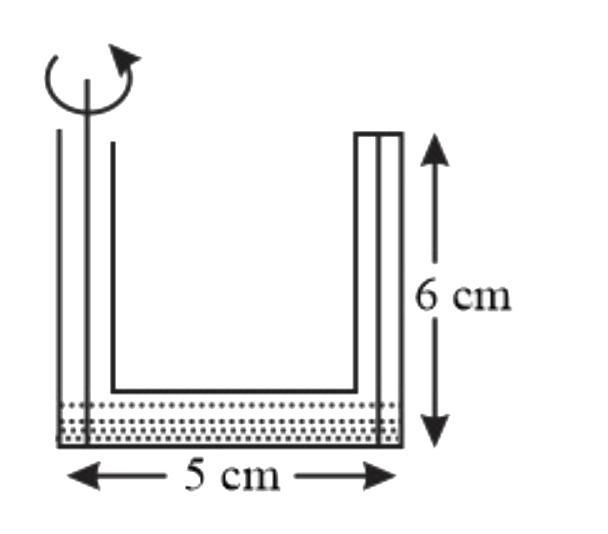
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then
A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If this expriment uses water instead of mercury , then
A. length of water will be equal to 76 cm
B. length of water will be less than 76 cm
C. length of water will be greater than 76 cm
D. none of the above
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mrcury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If a small hole is made at point P in the barometer tube , then
View Solution
