At what atomic number would a transition from n=2 to n=1 energy level result in emission of photon of λ=3×10−8m?
The correct Answer is:2
To solve the problem of determining the atomic number (Z) at which a transition from the n=2 to n=1 energy level results in the emission of a photon with a wavelength of λ = 3 x 10^(-8) m, we can use the Rydberg formula for hydrogen-like atoms. Here’s a step-by-step solution:
Step 1: Understand the Rydberg Formula
The Rydberg formula for the wavelength of emitted or absorbed light during electronic transitions in hydrogen-like atoms is given by:
1λ=RZ2(1n21−1n22)
Where:
- λ is the wavelength of the emitted photon,
- R is the Rydberg constant (R≈1.09×107m−1),
- Z is the atomic number,
- n1 and n2 are the principal quantum numbers of the initial and final states (with n2>n1).
Step 2: Substitute Known Values
In this case:
- n1=1
- n2=2
- λ=3×10−8m
Substituting these values into the formula gives:
1λ=RZ2(112−122)
Step 3: Calculate the Right Side
Calculate 112−122:
112−122=1−14=34
Step 4: Substitute into the Equation
Now substituting this back into the equation:
1λ=RZ2(34)
Step 5: Calculate 1λ
Calculate 1λ:
1λ=13×10−8=13×108m−1≈3.33×107m−1
Step 6: Set Up the Equation
Now we have:
3.33×107=1.09×107Z2(34)
Step 7: Solve for Z2
Rearranging gives:
Z2=3.33×1071.09×107×34
Calculating the denominator:
1.09×107×34=8.175×106
Now substituting back:
Z2=3.33×1078.175×106≈4.07
Step 8: Calculate Z
Taking the square root gives:
Z≈√4.07≈2.02
Since atomic numbers are whole numbers, we round this to:
Z=2
Final Answer
The atomic number at which a transition from n=2 to n=1 results in the emission of a photon with a wavelength of λ=3×10−8m is:
2
The Rydberg formula for the wavelength of emitted or absorbed light during electronic transitions in hydrogen-like atoms is given by:
- λ is the wavelength of the emitted photon,
- R is the Rydberg constant (R≈1.09×107m−1),
- Z is the atomic number,
- n1 and n2 are the principal quantum numbers of the initial and final states (with n2>n1).
In this case:
- n1=1
- n2=2
- λ=3×10−8m
Calculate 112−122:
Now substituting this back into the equation:
Calculate 1λ:
Now we have:
Rearranging gives:
Taking the square root gives:
The atomic number at which a transition from n=2 to n=1 results in the emission of a photon with a wavelength of λ=3×10−8m is:
Topper's Solved these Questions
Similar Questions
Estimate the difference in energy between first and second Bohr orbit for a hydrogen atom. At what minimum atomic number, a transition from n=2 to n=1 energy level would result in the emission of X-rays with λ=3.0×10−8m ? Which hydrogen-atom like species does this atomic number correspond to?
View SolutionEstimate the difference in energy between the first and second Bohr's orbit for a hydrogen atom At what minimum atomic number , a transition from n=2→n=1 energy level would result in the enmission of X -rays with λ=3.0×10−8m? Which hydogen -like spectrium does this atomic bnumber corresponding to ?
View Solution
Knowledge Check
- Question 1 - Select One
In hydrogen atom, electron makes transition from n=4 to n=1 level. Recoil momentum of the H atom will be
A3.4×10−27N−secB6.8×10−27N−secC3.4×10−24N−secD6.8×10−24N−sec - Question 2 - Select One
A hydrogen atom emits a photon corresponding to an electron transition from n=5 to n=1. The recoil speed of hydrogen atom is almost (mass of proton ≈1.6×10−27kg).
A10ms−1B2×10−2ms−1C4ms−1D8×102ms−1
For the hydrogen atom En=−1n2RH
Where RH=2.178×10−18J
Assuming that the electrons in other shells exert no effect, find the minimum no. of Z (atomit no.) at which a transition from the second energy level to the first results in teh emission of an X-ray. Given that the lowest energy rays have λ=4×10−8m.View SolutionIf the lowest energy X-rays have λ=3.055×10−8 m, estimate the minimum difference in energy between two Bohr's orbits such that an electronic transition would correspond to the emission of an X-ray. Assuming that the electrons in other shells exert no influence, at what Z (minimum) would a transition form the second level to the first result in the emission of an X-ray?
View SolutionA Bohr hydrogen atom at rest in free space undergoes a transition from the energy level n=2 to n=1, emitting a photon in the positive x direction. Since this photon has momentum, the atom must recoil in the negative x direction. Find the recoil velocity of the atom.
View SolutionThe energy levels of an atom are as shown in figure . Which one of those transition will result in the emission of a photon of wavelength 275nm?
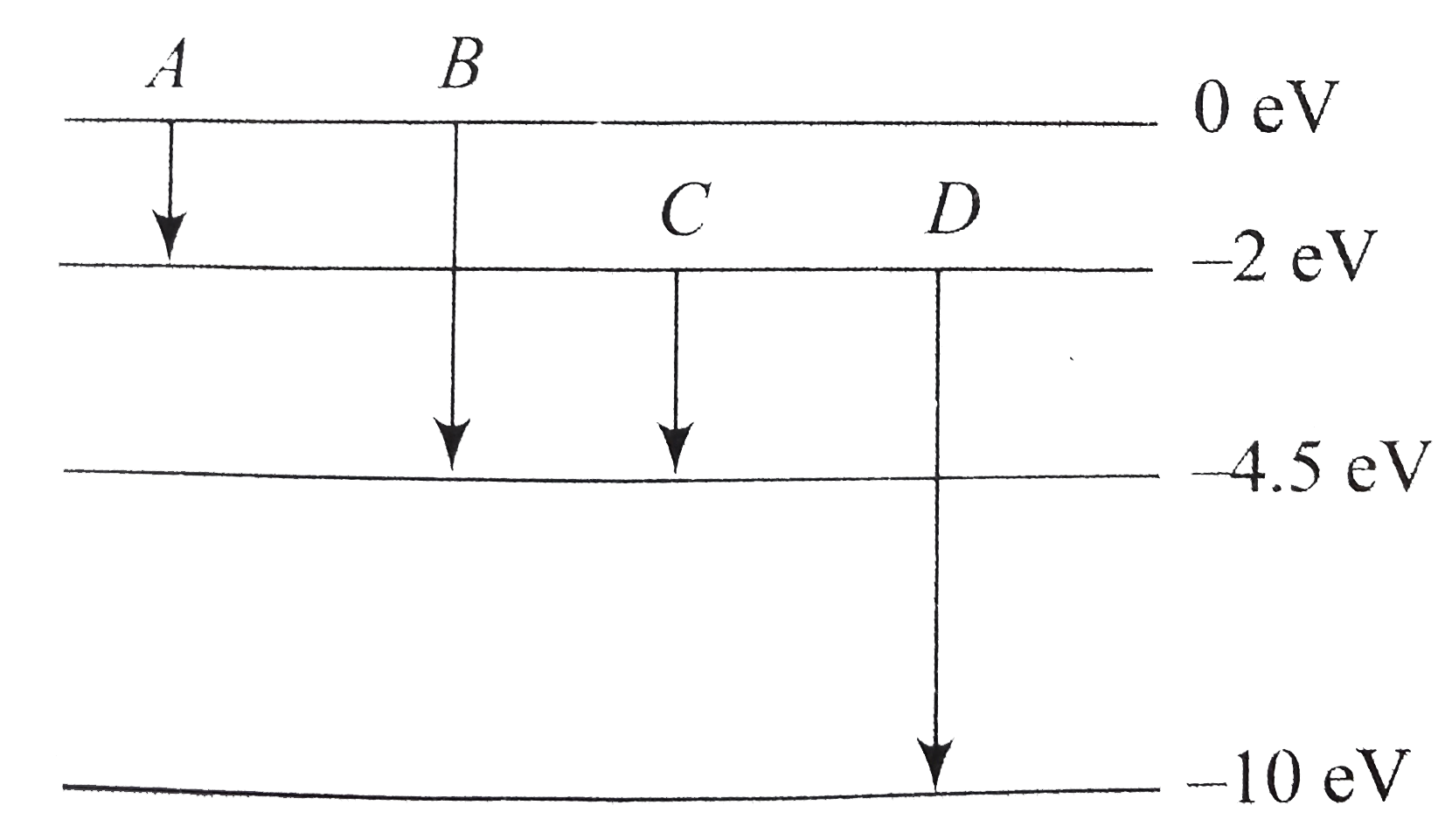 View Solution
View SolutionThe energy levels of an atom of element X are shown in the diagram. Which one of the level transitions will result in the emission of photons of wavelength 620 nm? Support your answer with mathematical calculations.
View SolutionA hydrogen atom a photon corresponding to an electron transition from n=5 to n=1 .The recoil speed of hydrogen atom is almost (mass of proton 1.6times10^(-27)kg) (A) 10m/s (B) 2times10^(-2)m/s (C) 4m/s
View Solution

