Calculate [ΘOH] of [NH2C2H4NH3]⊕ and [H3N−C2H4NH3]2+ in 0.15M ethylene diamine (aq) if
NH2C2H4NH2+H2O⇔NH2C2H4⊕NH3+ΘOH(K1=8.5×10−5)
NH2C2H4⊕NH3+H2O⇔[NH3C2H4NH3]2++ΘOH(K2=2.7×10−8)
To solve the problem, we need to calculate the concentration of hydroxide ions (OH−) produced from the two given reactions involving ethylene diamine and its ions. We will follow a step-by-step approach.
Step 1: Analyze the First Reaction
The first reaction is:
NH2C2H4NH2+H2O⇌NH2C2H4NH+3+OH−
The equilibrium constant K1 for this reaction is given as 8.5×10−5.
Let:
- The initial concentration of NH2C2H4NH2 be C=0.15M.
- The change in concentration at equilibrium be x.
At equilibrium:
- (NH2C2H4NH2)=C−x
- (NH2C2H4NH+3)=x
- (OH−)=x
Using the equilibrium expression:
K1=(NH2C2H4NH+3)(OH−)(NH2C2H4NH2)=x⋅xC−x=x20.15−x
Assuming x is small compared to 0.15, we can approximate C−x≈0.15:
K1=x20.15
Substituting the value of K1:
8.5×10−5=x20.15
Solving for x:
x2=8.5×10−5×0.15
x2=1.275×10−5
x=√1.275×10−5≈3.57×10−3M
Thus, the concentration of (OH−) from the first reaction is:
(OH−)=3.57×10−3M
Step 2: Analyze the Second Reaction
The second reaction is:
NH2C2H4NH+3+H2O⇌(H3N−C2H4NH3)2++OH−
The equilibrium constant K2 for this reaction is given as 2.7×10−8.
At equilibrium:
- Let y be the amount of NH2C2H4NH+3 that dissociates.
- The concentration of NH2C2H4NH+3 at equilibrium will be 3.57×10−3−y.
- The concentration of (H3N−C2H4NH3)2+ will be y.
- The concentration of (OH−) will be 3.57×10−3+y.
Using the equilibrium expression:
K2=(H3N−C2H4NH3)2+(OH−)(NH2C2H4NH+3)=y(3.57×10−3+y)3.57×10−3−y
Assuming y is small compared to 3.57×10−3:
K2≈y⋅3.57×10−33.57×10−3=y
Thus:
y=2.7×10−8M
Final Concentrations
1. The concentration of (OH−) from the first reaction is:
(OH−)=3.57×10−3M
2. The concentration of (H3N−C2H4NH3)2+ is:
(H3N−C2H4NH3)2+=2.7×10−8M
Summary of Results
- (OH−)≈3.57×10−3M
- (H3N−C2H4NH3)2+≈2.7×10−8M
NH2C2H4NH2+H2O⇌NH2C2H4NH+3+OH−
The equilibrium constant K1 for this reaction is given as 8.5×10−5.
- The initial concentration of NH2C2H4NH2 be C=0.15M.
- The change in concentration at equilibrium be x.
- (NH2C2H4NH2)=C−x
- (NH2C2H4NH+3)=x
- (OH−)=x
K1=(NH2C2H4NH+3)(OH−)(NH2C2H4NH2)=x⋅xC−x=x20.15−x
K1=x20.15
Substituting the value of K1:
8.5×10−5=x20.15
Solving for x:
x2=8.5×10−5×0.15
x2=1.275×10−5
x=√1.275×10−5≈3.57×10−3M
(OH−)=3.57×10−3M
NH2C2H4NH+3+H2O⇌(H3N−C2H4NH3)2++OH−
The equilibrium constant K2 for this reaction is given as 2.7×10−8.
- Let y be the amount of NH2C2H4NH+3 that dissociates.
- The concentration of NH2C2H4NH+3 at equilibrium will be 3.57×10−3−y.
- The concentration of (H3N−C2H4NH3)2+ will be y.
- The concentration of (OH−) will be 3.57×10−3+y.
K2=(H3N−C2H4NH3)2+(OH−)(NH2C2H4NH+3)=y(3.57×10−3+y)3.57×10−3−y
K2≈y⋅3.57×10−33.57×10−3=y
Thus:
y=2.7×10−8M
(OH−)=3.57×10−3M
(H3N−C2H4NH3)2+=2.7×10−8M
- (OH−)≈3.57×10−3M
- (H3N−C2H4NH3)2+≈2.7×10−8M
Topper's Solved these Questions
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Exercises Subjective (Buffer Solutions)
2 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Exercises Subjective (Hydrolysis Of Salt)
2 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.5
6 Videos
- HYDROGEN, WATER AND HYDROGEN PEROXIDEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - HYDROGEN, WATER AND HYDROGEN PEROXIDEEXERCISE - Subjective Archive (Subjective)
3 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type
1 Videos
Similar Questions
Knowledge Check
CH3CH2CH2−O∣∣C−H+CH3−C≡ChNa,NH3(l)−−−−−−−→
A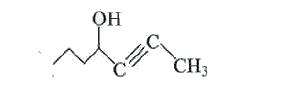 B
B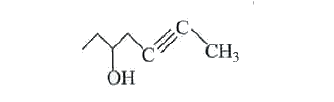 C
C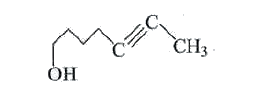 D
D
NH4Cl+NaNO2Δ−−→N2↑⏐⏐+NaCl+H2O
View SolutionNH4Cl+NaNO2Δ−−→N2↑⏐⏐+NaCl+H2O
View Solution(NH4)2Cr2O7Δ−−→N2↑⏐⏐+Cr2O3⏐⏐↓+H2O↑⏐⏐
View Solution(NH4)2Cr2O7Δ−−→N2↑⏐⏐+Cr2O3⏐⏐↓+H2O↑⏐⏐
View SolutionCalculate the molecular masses of H2,O2,Cl2,CO2,CH4,C2H6,C2H4,NH3,CH3OH.
View SolutionNH4OH,NaOH,CH3COOH,H2S
View SolutionIf N2+3H2K⇐⇒2NH3 then 2N2+6H2K'⇐⇒4NH3;K' is equal to
View Solution
