Calculate the degree of ionization of dimethylamine in its 0,02 M solution. Kb=5.4×10−4. What percentage of dimethylamine is ionized if the solution is also 0.01 M in NaOH ?
The correct Answer is:0.164,0.0054
To solve the problem of calculating the degree of ionization of dimethylamine in a 0.02 M solution and the percentage of ionization when 0.01 M NaOH is also present, we can follow these steps:
Step 1: Write the ionization equation for dimethylamine
Dimethylamine (CH₃)₂NH can ionize in water as follows:
(CH₃)₂NH+H2O⇌(CH₃)₂NH+2+OH−
Step 2: Set up the equilibrium expression
The base dissociation constant Kb for dimethylamine is given by:
Kb=((CH₃)₂NH+2)(OH−)((CH₃)₂NH)
Given Kb=5.4×10−4 and the initial concentration of dimethylamine is 0.02 M, we can set up the expression at equilibrium.
Step 3: Define the changes in concentration
Let x be the amount of dimethylamine that ionizes. At equilibrium:
- The concentration of (CH₃)₂NH will be 0.02−x
- The concentration of (CH₃)₂NH+2 and OH− will both be x
Step 4: Substitute into the equilibrium expression
Substituting into the Kb expression:
5.4×10−4=x⋅x0.02−x≈x20.02
(We can approximate 0.02−x≈0.02 because x will be small.)
Step 5: Solve for x
Rearranging gives:
x2=5.4×10−4×0.02
x2=1.08×10−5
x=√1.08×10−5≈0.00329M
Step 6: Calculate the degree of ionization
The degree of ionization (α) is given by:
α=xC0=0.003290.02≈0.1645
Step 7: Convert to percentage
To find the percentage of ionization:
Percentage of ionization=α×100≈16.45%
Step 8: Consider the effect of NaOH
When 0.01 M NaOH is added, the concentration of OH− increases. This will shift the equilibrium to the left due to the common ion effect.
Step 9: Set up the new equilibrium expression
Now, the equilibrium expression becomes:
Kb=(0.01+x)(x)0.02−x
Assuming x is small compared to 0.01, we can approximate:
Kb=0.01⋅x0.02
Substituting Kb:
5.4×10−4=0.01⋅x0.02
Step 10: Solve for x again
Rearranging gives:
x=5.4×10−4⋅0.020.01=1.08×10−3M
Step 11: Calculate the new degree of ionization
Now calculate the new degree of ionization:
α=xC0=1.08×10−30.02=0.054
Step 12: Convert to percentage
Finally, convert to percentage:
Percentage of ionization=0.054×100≈5.4%
Final Answer
The degree of ionization of dimethylamine in a 0.02 M solution is approximately 16.45%, and the percentage of dimethylamine ionized in a solution that is also 0.01 M in NaOH is approximately 5.4%.
---
Dimethylamine (CH₃)₂NH can ionize in water as follows:
(CH₃)₂NH+H2O⇌(CH₃)₂NH+2+OH−
The base dissociation constant Kb for dimethylamine is given by:
Kb=((CH₃)₂NH+2)(OH−)((CH₃)₂NH)
Given Kb=5.4×10−4 and the initial concentration of dimethylamine is 0.02 M, we can set up the expression at equilibrium.
Let x be the amount of dimethylamine that ionizes. At equilibrium:
- The concentration of (CH₃)₂NH will be 0.02−x
- The concentration of (CH₃)₂NH+2 and OH− will both be x
Substituting into the Kb expression:
5.4×10−4=x⋅x0.02−x≈x20.02
(We can approximate 0.02−x≈0.02 because x will be small.)
Rearranging gives:
x2=5.4×10−4×0.02
x2=1.08×10−5
x=√1.08×10−5≈0.00329M
The degree of ionization (α) is given by:
α=xC0=0.003290.02≈0.1645
To find the percentage of ionization:
Percentage of ionization=α×100≈16.45%
When 0.01 M NaOH is added, the concentration of OH− increases. This will shift the equilibrium to the left due to the common ion effect.
Now, the equilibrium expression becomes:
Kb=(0.01+x)(x)0.02−x
Assuming x is small compared to 0.01, we can approximate:
Kb=0.01⋅x0.02
Substituting Kb:
5.4×10−4=0.01⋅x0.02
Rearranging gives:
x=5.4×10−4⋅0.020.01=1.08×10−3M
Now calculate the new degree of ionization:
α=xC0=1.08×10−30.02=0.054
Finally, convert to percentage:
Percentage of ionization=0.054×100≈5.4%
The degree of ionization of dimethylamine in a 0.02 M solution is approximately 16.45%, and the percentage of dimethylamine ionized in a solution that is also 0.01 M in NaOH is approximately 5.4%.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - Conceptual Question 124videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - Conceptual Question 215videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - Unit Practice Test13videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - ENVIRONMENTAL POLLUTION EXERCISE - UNIT PRACTICE TEST15videos
ENVIRONMENTAL POLLUTION
- BOOK - MODERN PUBLICATIONCHAPTER - HALOALKANES AND HALOARENESEXERCISE - UNIT PRACTICE TEST12videos
HALOALKANES AND HALOARENES
Similar Questions
The ionisation constant of dimethylamine is 5.4×10−4. Calculate its degree of ionization in its 0.02M solution. What percentage of dimethylamine is ionized if the solution is also 0.1M in NaOH?
View SolutionThe ionisation constant os dimethylamine is 5.4×10−4. Calculate its degree of ionization in its 0.02M solution. What percentage of dimethylamine is ionized if the solution is also 0.1M in NaOH?
View Solution
Knowledge Check
- Question 1 - Select One
Calculate the degree of hydrolysis of the 0.01 M solution of salt(KF)(Ka(HF)=6.6×10−4) :-
A3.87×10−6B3.87×10−5C3.87×10−2DNone of these - Question 2 - Select One
The degree of ionization of 0.10 M lactic acid is 4.0%
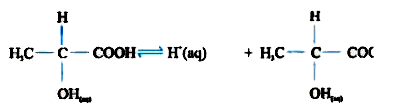
The value of KCA1.66×10−5B1.66×10−4C1.66×10−3D1.66×10−2
The ionization constant of propanoic acid is 1.32×10−5. Calculate the degree of ionization of the acid in its 0.05M solution and also its pH. What will be its degree of ionization if the solution is 0.01M on HCl also?
View SolutionThe ionization constant of propionic acid is 1.32×10−5. Calculate the degree of ionization of the acid in its 0.05M solution and also its pH. What will be its degree of ionization in the solution of 0.01NHCI ?
View SolutionThe ionization constant of acetic acid 1.74×10−5. Calculate the degree of dissociation of acetic acid in its 0.05M solution. Calculate the concentration of acetate ion in the solution and its pH.
View SolutionThe ionization constant of acetic acid 1.74×10−5. Calculate the degree of dissociation of acetic acid in its 0.05M solution. Calculate the concentration of acetate ion in the solution and its pH.
View SolutionThe ionization constant of HF is 3.2×10−4. Calculate the degree of ionization of HF in its 0.02M solution. Calculate the concentration of all species present in the solution and its pH.
View SolutionThe ionization constant of propanoic acid is 1.32×10−5. Calculate the degree of ionization of the acid in its 0.05M solution and also its pH. What will be its degree of ionization if the solution is 0.01M on HCl also?
View Solution

