Calculate the molarity of water if its density is 1000kgm−3
To calculate the molarity of water given its density of 1000 kg/m³, we can follow these steps:
Step 1: Understand the relationship between density, mass, and volume
Density (ρ) is defined as mass (m) per unit volume (V). The formula is:
ρ=mV
Given that the density of water is 1000 kg/m³, we can convert this to grams per liter (since 1 kg = 1000 g and 1 m³ = 1000 L):
1000kg/m3=1000g/L
Step 2: Calculate the mass of water in 1 liter
From the density, we know that 1 liter of water has a mass of:
m=1000g
Step 3: Determine the molar mass of water
The molar mass of water (H₂O) is approximately:
Molar mass of H2O=2×1g/mol (for H)+16g/mol (for O)=18g/mol
Step 4: Calculate the number of moles of water in 1 liter
Using the formula for the number of moles (n):
n=mMolar mass=1000g18g/mol≈55.56mol
Step 5: Calculate the molarity of water
Molarity (M) is defined as the number of moles of solute per liter of solution. Since we have calculated the number of moles in 1 liter of water:
M=nV=55.56mol1L=55.56M
Final Answer
The molarity of water is approximately:
Molarity of water≈55.56M
---
Density (ρ) is defined as mass (m) per unit volume (V). The formula is:
ρ=mV
Given that the density of water is 1000 kg/m³, we can convert this to grams per liter (since 1 kg = 1000 g and 1 m³ = 1000 L):
1000kg/m3=1000g/L
From the density, we know that 1 liter of water has a mass of:
m=1000g
The molar mass of water (H₂O) is approximately:
Molar mass of H2O=2×1g/mol (for H)+16g/mol (for O)=18g/mol
Using the formula for the number of moles (n):
n=mMolar mass=1000g18g/mol≈55.56mol
Molarity (M) is defined as the number of moles of solute per liter of solution. Since we have calculated the number of moles in 1 liter of water:
M=nV=55.56mol1L=55.56M
The molarity of water is approximately:
Molarity of water≈55.56M
Topper's Solved these Questions
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Fill In The Blanks
4 Videos
- S-BLOCK GROUP 2 - ALKALINE EARTH METALSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - S-BLOCK GROUP 2 - ALKALINE EARTH METALSEXERCISE - Ex 5.1 Objective
2 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises (Ture False)
25 Videos
Similar Questions
Knowledge Check
At What velocity does water emerge from an orifice in a tank in which gauge pressure is 3×105Nm−2 before the flow starts ? (Take the density of water =1000kgm−3.)
A24.5ms−1B14.5ms−1C34.5ms−1D44.5ms−1
The area of base of a cylindrical vessel is 300cm2.
Water (density= 1000kg/m3) is poured into it up to a depth of 6 cm. Calculate the thrust of water on the base. (g=10m s−2).
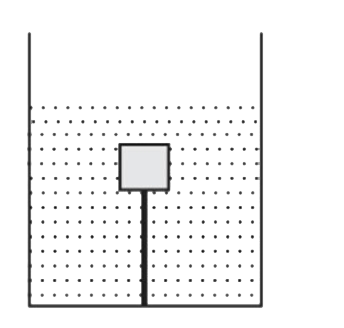
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
View SolutionThe wire of a Young's modules appartus is elongated by 2 mm when a brick is suspended from .it When the brick is immersed in water the wire contracts by 0.6mm Calculate the density of the brick given that the density of water is 1000kgm−3
View SolutionA rectangular tank of base area 100 m2 has a height of 2 m. Calculate the thrust at the bottom of the tank, if it is filled upto the brim with water of density 103 kg m−3.
View SolutionThe lower end of a clean glass capillary tube of internal radius 2×10−4m is dippled into a beaker containing water . The water rise up the tube to a vertical height of 7×10−2m above its level in the beaker. Calculate the surface tension of water. Density of water = 1000kgm−3,g=10ms−2 .
View SolutionWater is flowing through a horizontal tube of length 0.25 m and radius 4×10−4 m under a constant pressure head of 0.2 m of water, at the rate of 5×10−6m3 per minutre . Calculate the coefficient of visosity of water. Density of water = 1000 kg m−3
View Solution1gcm−3=1000kgm−3
View Solution

