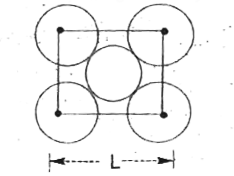
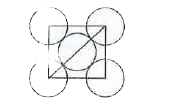
Calculate the packing efficiency of the two-dimensional square unit cells as given in the figure. Solution in Bengali
Each corner sphere of the unit cell is equally shared by 4 adjoining unit cells. So, each corner sphere makes a contribution of 1/4 to the unit cell. The sphere at the centre of the unit cell is not shared by other unit cells, so its contribution to the unit cell is 1. Number of corners of the unit cell is 4.

Total number of particles per unit cell = 4×14+1=2
Area of each sphere is πr2, where r = radius of the sphere.
Total area for two particles in the unit cell = 2πr2
The area of the unit cell = a2. From the figure it is evident,
AB=√AC2+CB2=√a2+a2=a√2=4r
∴4r=a√2or,a=2√2r
Hence, packing fraction = Total area of 2 spheresArea of the unit cell×100
=2πr2a2×100=2πr2(2√2r)2=78.5%
Topper's Solved these Questions
- SOLID STATEBOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - SOLVED WBCHSE SCANNER
8 Videos
- SOLID STATEBOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - SOLVED CBSE SCANNER
21 Videos
- SOLID STATEBOOK - CHHAYA PUBLICATIONCHAPTER - SOLID STATEEXERCISE - WARM UP EXERCISE
70 Videos
- PREVIOUS YEARS QUESTION PAPER 2019BOOK - CHHAYA PUBLICATIONCHAPTER - PREVIOUS YEARS QUESTION PAPER 2019EXERCISE - WBCHSE 2019 PART-B
19 Videos
- SOME p-BLOCK ELEMENTSBOOK - CHHAYA PUBLICATIONCHAPTER - SOME p-BLOCK ELEMENTSEXERCISE - PRACTIVE SET 11
15 Videos
Similar Questions
(i) Which type of semiconductor is sillicon having arsenic as impurity?
(ii) An elements (density = 7.2g⋅cm−3) crystallises in a body-centred cubic structure having its cell edge length 2.88Å. Calculate the number of atoms and the number of unit cells present in 156g of the element.
View SolutionWhat is meant by 'doping' in a semiconductor?
View SolutionWhy does a solid substance possess a definite shape & volume?
View SolutionWhich of the following is strongly attracted by magnetic field /
View SolutionHow will you separate CO and CO2 from a mixture?
View SolutionThe packing efficiency of a two-dimensional square unit cell shown below is
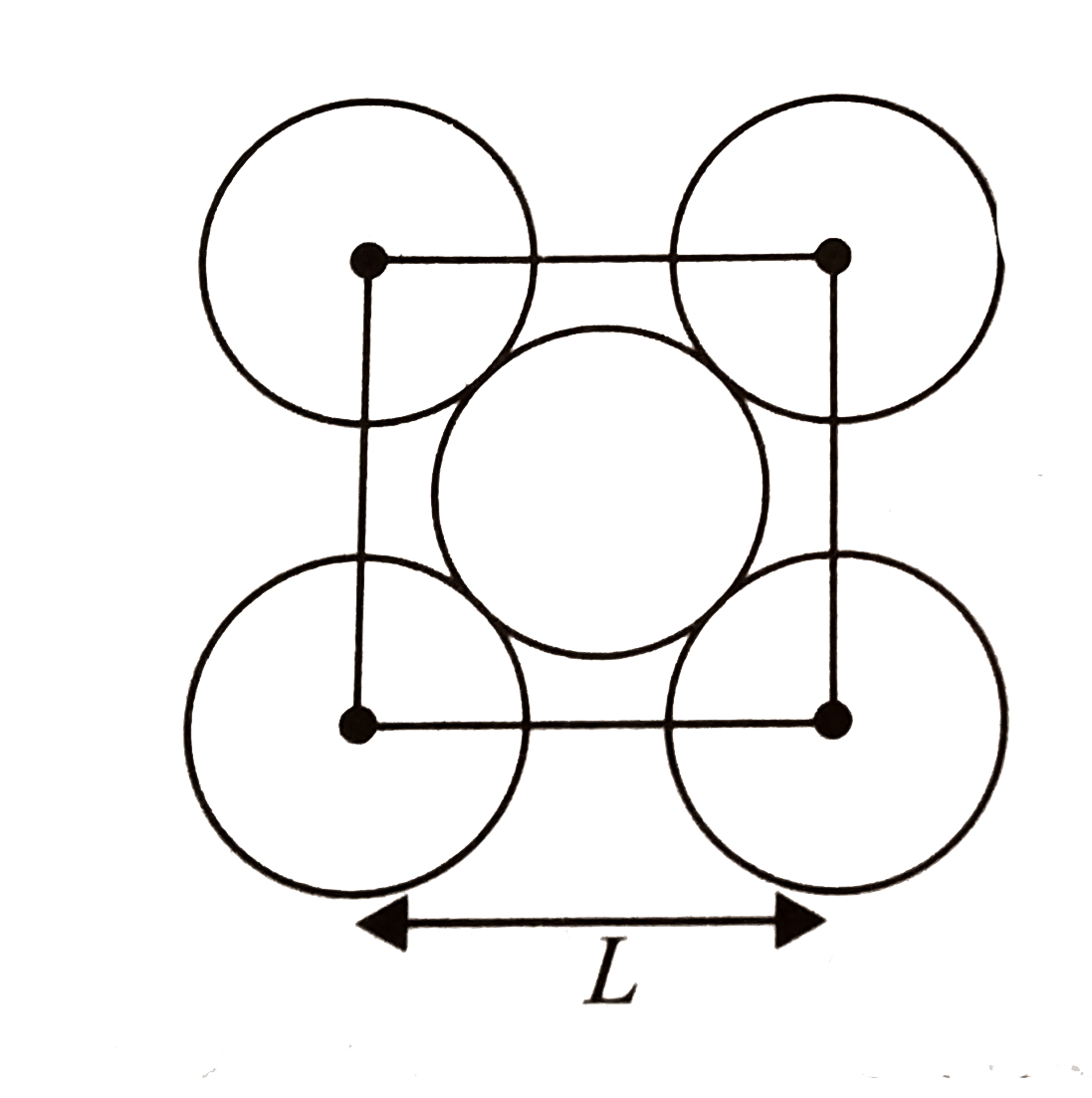
View SolutionThe packing efficiency of the two dimensional square unit cell shown below is:
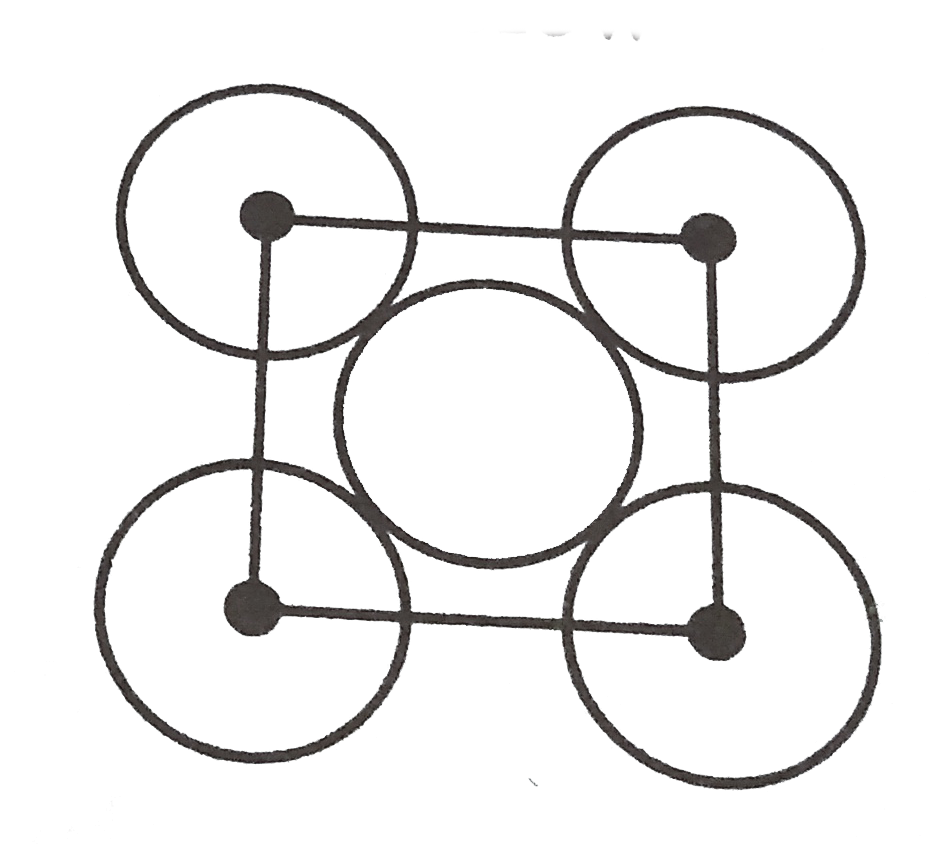
View SolutionThe packing effciency of the two dimensional cell square unit as shown is

View SolutionThe packing efficiency of the two dimensional square unit cell show in the adjoining fig ,. Is
(##PR_CHE_V01_XII_C01_E20_009_Q01.png" width="80%">
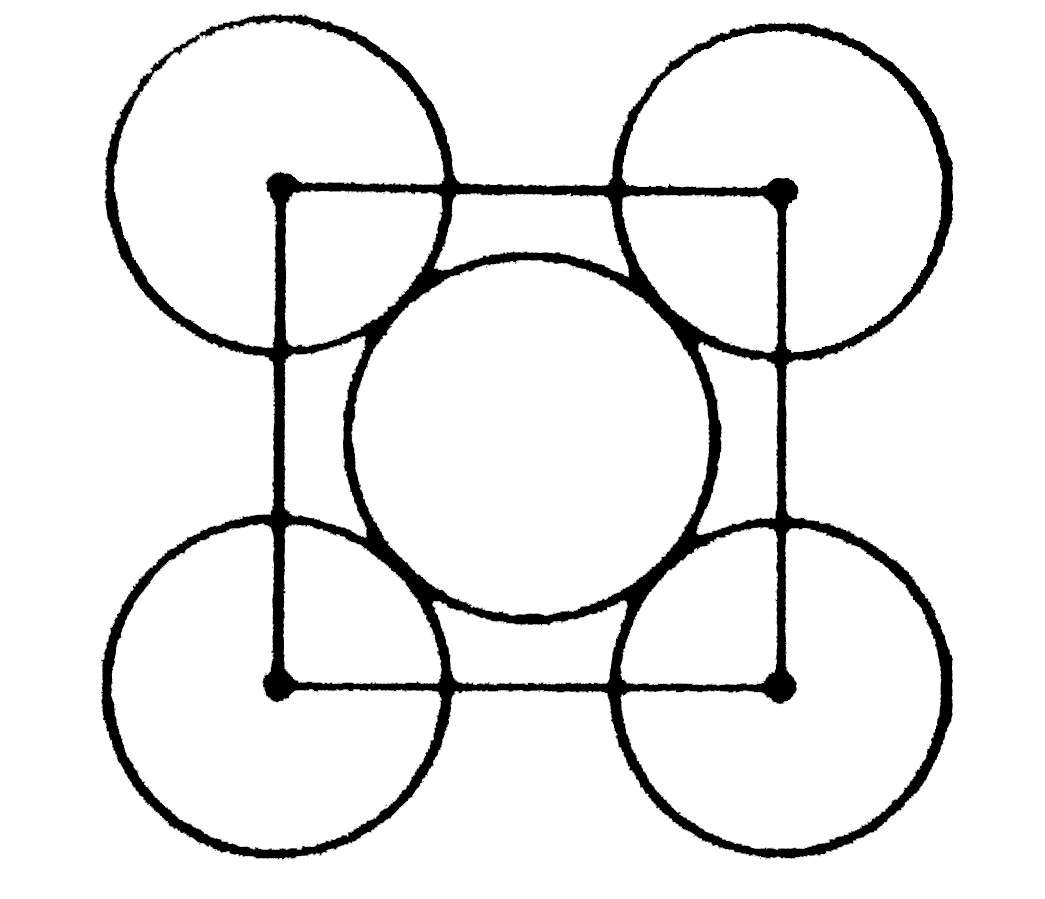
View SolutionThe packing efficiency of the two-dimensional sqare unit cell shown below is
View SolutionCalculate packing efficiency in simple cubic unit cell.
View SolutionThe packing efficiency of the two - dimensional square unit cell show below is
View SolutionCalculate the packing efficiency in fcc unit cell ?
View SolutionThe packing efficiency of the two dimensional square unit cell shown is :
View SolutionThe packing efficiency of the two dimensional square unit cell shown below is
View Solution
