Consider the following statements Then .
is independent of temperature
is equal to to Boyle temperature
has the dimension of molar volume
None of these
At Boyle' s temperature .
Topper's Solved these Questions
- GASEOUS STATEBOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise B
1 Videos
- GASEOUS STATEBOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise 4
1 Videos
- GASEOUS STATEBOOK - P BAHADURCHAPTER - GASEOUS STATEEXERCISE - Exercise 3
1 Videos
- CHEMICAL EQUILIBRIUMBOOK - P BAHADURCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise
134 Videos
- IONIC EQUILIBRIUMBOOK - P BAHADURCHAPTER - IONIC EQUILIBRIUMEXERCISE - Exercise
85 Videos
Similar Questions
For a real gas with very large value of molar volume, which of the following equation can most suitably be applied:
(A) Z = 1 -aVmRT
(B) PV =RT
(C) Z = 1+ PbRT
(D) PVm-RT = aVm
View SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
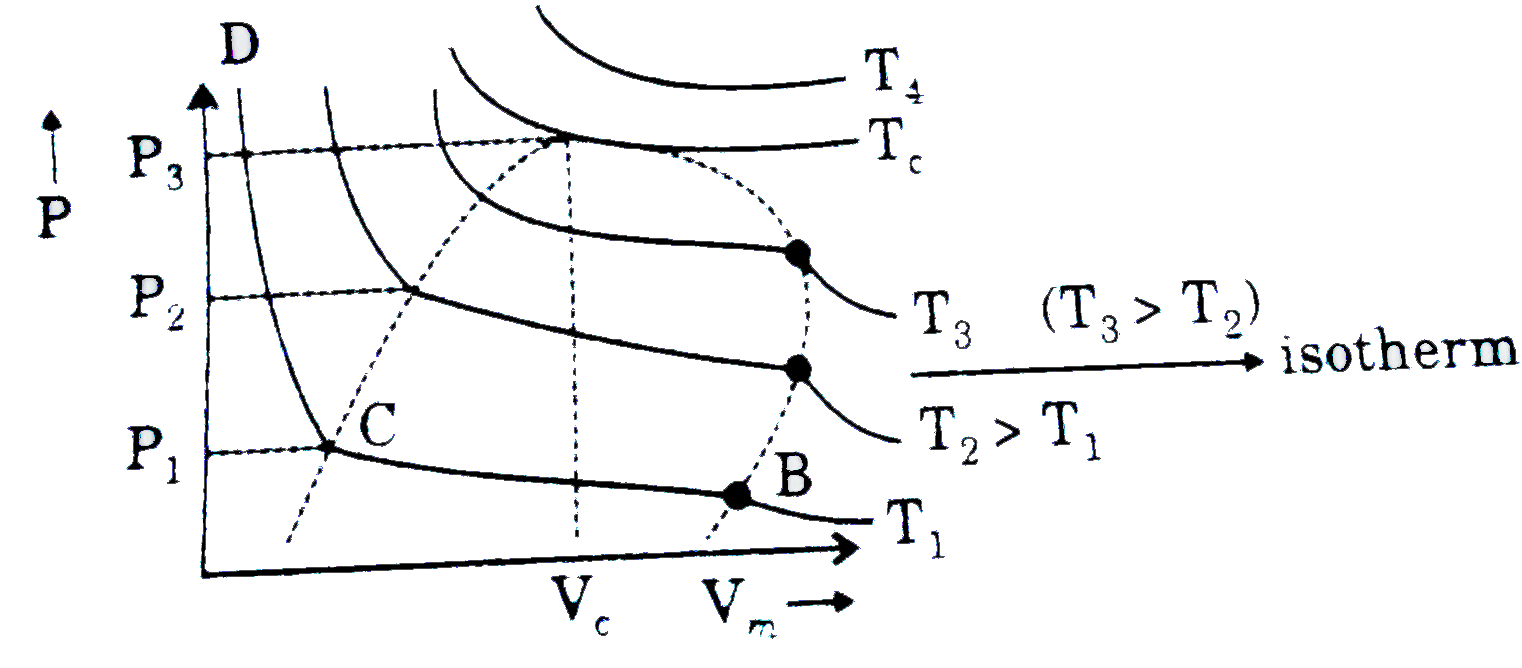
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
A scientist proposed the following equation of state
P=RTVm−BV2m+CV2m If this equation leads to the critical behaviour then critical temperature is
View Solution
Knowledge Check

When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

A scientist proposed the following equation of state P=RTVm−BV2m+CV3m. If this equation leads to teh critical behaviour then critical temperature is:A8B27RCBB8RCCB23RCDNone of theseConsider the following statements: The coefficient B in the virial equation of state
(P) is independent of temperature
(Q) is equal to zero at boyle temperature
PVm=RT(1+BVm+CV2m+......)
(R) has the dimension of molar volume which of the above statement are correct?AP and QBP and RCQ andRDP,Q and Rvan der Waal's equation of state for real gases may be written as:
PVm=RT(1+BVm+CV2m+....)
Select the correct statement(s).AB' and C are temperature dependent.BB' is temperature dependent while 'C' is temperature independent.CB' may be positive negative or zero.DB' may be positive and 300 K is performing 4×109 collisions per sec per O2 molecule. Select the correct statement(s): Given: [NA=6×1023]
According to virial equation of state for 1 mole of a real gas
PVM=RT[A+BVM+CV2M+...] which one is not correct ? .
View SolutionFor a non-ideal gas, the compressibility factor (Z) is defined as:
Z=pVmRT,Vm= Molar volume
Compressibility of an unknown gas at 600K and 1.0 atm was found to be 1.2 Also this gas was found to effuse 1.58 times slower than the pure methane gas under identical condition. Answer the following three questions based on the above mentioned information and the information provided in an individual question.
The value of the Virial coefficient 'B' in the Virial equation is,
(Ignore the higher terms from equation during calculation)
Virial equation : Z=1+BVm+CV2m+DV3m+.........,Vm is the molar volume
View SolutionVirial equation is: PVM=RT[A+BVM+CVM2+…], where A, B, C, …. are first second,third, … virial coefficent, respectively, For an ideal gas
View Solution
When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

Identify the wrong statement related to the above graph:

View SolutionThe van der Waals' equation for one mole may be expressed as
V3M−(b+RTP)V2m+aVmP−abP=0
where Vm is the molar volume of the gas. Which of the followning is incorrect?
View Solution
