Derive a mathematical expression showing the relationship between the extent of adsorption of a gas on a suface with pressure (within lower and higher ranges). Calculate the extent of adsorption at one atmosphere.
To derive the mathematical expression showing the relationship between the extent of adsorption of a gas on a surface with pressure, we will use the Freundlich adsorption isotherm. The Freundlich isotherm is a model that describes how the amount of gas adsorbed on a solid surface varies with the pressure of the gas.
Step 1: Write the Freundlich Adsorption Isotherm Equation
The Freundlich adsorption isotherm is given by the equation:
xm=kp1n
Where:
- x = mass of gas adsorbed
- m = mass of the adsorbent
- p = pressure of the gas
- k = Freundlich constant (a measure of adsorption capacity)
- n = Freundlich constant (related to the adsorption intensity)
Step 2: Analyze the Equation for Low Pressure (p → 0)
At low pressures, the extent of adsorption is directly proportional to the pressure. If we assume n>1:
xm=kp1n
As p approaches 0, the term p1n also approaches 0, indicating that the extent of adsorption increases with increasing pressure.
Step 3: Analyze the Equation for High Pressure (p → ∞)
At high pressures, the adsorption reaches a saturation point, and the extent of adsorption becomes independent of pressure. In this case, we can simplify the equation. As p becomes very large, p1n approaches a constant value:
xm=kp1n→constant
This indicates that at high pressures, the extent of adsorption does not change significantly with further increases in pressure.
Step 4: Calculate the Extent of Adsorption at One Atmosphere
To calculate the extent of adsorption at one atmosphere (1 atm), we substitute p=1 into the Freundlich equation:
xm=k(1)1n=k
Thus, the extent of adsorption at 1 atmosphere is simply equal to k.
Final Expression
In summary, the relationship between the extent of adsorption and pressure can be summarized as follows:
- At low pressures: xm∝p
- At high pressures: xm approaches a constant value.
At 1 atmosphere, the extent of adsorption is:
xm=k
The Freundlich adsorption isotherm is given by the equation:
- x = mass of gas adsorbed
- m = mass of the adsorbent
- p = pressure of the gas
- k = Freundlich constant (a measure of adsorption capacity)
- n = Freundlich constant (related to the adsorption intensity)
At low pressures, the extent of adsorption is directly proportional to the pressure. If we assume n>1:
At high pressures, the adsorption reaches a saturation point, and the extent of adsorption becomes independent of pressure. In this case, we can simplify the equation. As p becomes very large, p1n approaches a constant value:
To calculate the extent of adsorption at one atmosphere (1 atm), we substitute p=1 into the Freundlich equation:
In summary, the relationship between the extent of adsorption and pressure can be summarized as follows:
- At high pressures: xm approaches a constant value.
Topper's Solved these Questions
- SURFACE CHEMISTRY BOOK - PRADEEPCHAPTER - SURFACE CHEMISTRY EXERCISE - SHORT ANSWER QUESTIONS (II. CATALYSIS)
9 Videos
- SURFACE CHEMISTRY BOOK - PRADEEPCHAPTER - SURFACE CHEMISTRY EXERCISE - SHORT ANSWER QUESTIONS (III. COLLOIDS)
43 Videos
- SURFACE CHEMISTRY BOOK - PRADEEPCHAPTER - SURFACE CHEMISTRY EXERCISE - ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS)
55 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - PRADEEPCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Competition (FOCUS) JEE (Main and Advanced)/Medical Entrance SPECIAL (VIII. Assertion-Reason Type Questions)(Type II)
13 Videos
Similar Questions
Derive the mathematical expression or show the relationship between the extent of a adsorption of a gas on the surface of a solid (with lower and higher ranges of pressure). Calculate the extent of adsorption at one atmosphere.
View SolutionA cusrve showing the variation of extent of adsorption with temperature at constant pressure is called……………
View Solution
Knowledge Check
If the pressure of a gas is increased, its extent of adsorption will
AdecreaseBincrease in all pressuresCincrease at low pressure onlyDdecrease at high pressuresA graph is plotted between extent of adsorption vs pressure (P) at constant temperature, the Frendlich equation at points A, B, C respectively are:
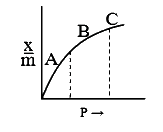 Axm=kp,xm=kp1/n,xm=kpoBxm=kp,xm=kpn,xm=kp1/nC(x)/(m)=kp^(1//n),(x)/(m)=kp^(n),(x)/(m)=kp^(1//n)Dxm=kp∞,xm=kp1/n,xm=kpn
Axm=kp,xm=kp1/n,xm=kpoBxm=kp,xm=kpn,xm=kp1/nC(x)/(m)=kp^(1//n),(x)/(m)=kp^(n),(x)/(m)=kp^(1//n)Dxm=kp∞,xm=kp1/n,xm=kpnLangmuir's adsorption equation which describes the amount of gas adsorbed on a solid surface is written as
Px/m=1ab+Pb
where x/m is the extent of adsorption, a and b are constants and P is the gas pressure. On the basis of the above equation indicate which of the following statements is correct ?AAt low vslue of P,x/m∝PBAt high value of P,xm→a/b (i.e adsorption is indenpendent of pressure)CBetween the low and high values of P , the above equation becomes x/m=kP1/n , which is the Freundlich equation (here K and n are constant).DAll of these
How do size of particles of adsorbent, pressure of gas and prevailling temperature influence the extent of adsorption of a gas on a solid ?
View SolutionHow do size of particles of adsorbent, pressure of gas and prevailling temperature influence the extent of adsorption of a gas on a solid ?
View SolutionHow do size of particles of adsorbent, pressure of gas, and prenvailing temperature influence the extent of adsorption of a gas on a solid?
View SolutionState whether the following statements are True or False
(i) Accounting ratio is a mathematical expression of relationship between two items or group of items in the financial statements
(ii) Price level changes are igonred in ratio analysis. It is an advantage of Ratio Analysis.
(iii) Quick Ratio establishes the relationship between current assets and current liabilities
(iv) In calculating Debt-Equity ratio, all external debts are considered.
(v) Debit balance in Surplus i.e., Balance in Statement of Profit and Loss is not deducted to calculate Shareholder's Funds to calculate Debt-Equity Ratio.
(vi) The objective of calculating Proprietary Ratio is to measure proportion of fixed assets financed by the Shareholder's Funds.
(vii) In Debt to Total Assets Ratio, debt includes only long-term Borrowings and Long-term Provisions.
(viii) Interest Coverage ratio shows the amount of profit available to cover the interest.
(ix) The formula for Trade Payables Turnover Ratio is Net Credit Purchases/Average Trade Receivables.
(x) Loose tools and Stores and Spares are excluded to calculate Working Capital to calculate Working Capital Turnover Ratio.
(xi) Gross profit helps in fixing selling prices and assessing efficiency of trading activities.
View SolutionDefine adsorption isotherm. Give the empirical relationship between the quantity of gas adsorbed by unit mass of solid absorbent and pressure at a particular temperature.
View Solution
