Energy of activation of forward and backward reaction are equal in case (numerical calues) where
ΔH=0
No catalyst present
ΔS=0
Stoichiometry is the mechanism
The correct Answer is:A
To solve the question regarding the conditions under which the energy of activation of the forward and backward reactions are equal, we can follow these steps:
1. Understanding Activation Energy:
- Activation energy (Ea) is the minimum energy required for a reaction to occur. For a reaction, we have two activation energies: one for the forward reaction (Ea forward) and one for the backward reaction (Ea backward).
2. Using the Relationship:
- The relationship between the activation energies and the change in enthalpy (ΔH) of the reaction can be expressed as:
ΔH=Eforwarda−Ebackwarda
3. Setting the Activation Energies Equal:
- According to the problem, we are given that the activation energies for the forward and backward reactions are equal. Let's denote both activation energies as x:
Eforwarda=xandEbackwarda=x
4. Substituting into the Equation:
- Substituting these values into the ΔH equation gives:
ΔH=x−x=0
5. Conclusion:
- Since ΔH equals zero, this indicates that the enthalpy change for the reaction is zero. This typically occurs in a reaction that is at equilibrium, where the energy required to break bonds in the reactants is equal to the energy released when new bonds are formed in the products.
6. Identifying the Correct Option:
- The only scenario where the activation energies of both the forward and backward reactions are equal, leading to a change in enthalpy of zero, is option A.
Final Answer:
- The correct option is A, where the activation energy of the forward and backward reactions are equal, resulting in a change in enthalpy (ΔH) of zero.
- Activation energy (Ea) is the minimum energy required for a reaction to occur. For a reaction, we have two activation energies: one for the forward reaction (Ea forward) and one for the backward reaction (Ea backward).
- The relationship between the activation energies and the change in enthalpy (ΔH) of the reaction can be expressed as:
ΔH=Eforwarda−Ebackwarda
- According to the problem, we are given that the activation energies for the forward and backward reactions are equal. Let's denote both activation energies as x:
Eforwarda=xandEbackwarda=x
- Substituting these values into the ΔH equation gives:
ΔH=x−x=0
- Since ΔH equals zero, this indicates that the enthalpy change for the reaction is zero. This typically occurs in a reaction that is at equilibrium, where the energy required to break bonds in the reactants is equal to the energy released when new bonds are formed in the products.
- The only scenario where the activation energies of both the forward and backward reactions are equal, leading to a change in enthalpy of zero, is option A.
- The correct option is A, where the activation energy of the forward and backward reactions are equal, resulting in a change in enthalpy (ΔH) of zero.
Topper's Solved these Questions
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Single Correct Answer Type
2 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Exercises Assertion-Reasoning
17 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Exercises Multiple Correct
25 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
- SYNTHETIC AND NATURAL POLYMERSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SYNTHETIC AND NATURAL POLYMERSEXERCISE - Exercises Assertion Reasoning
10 Videos
Similar Questions
When the activation energies of the forward and backward reactions are equal, then :
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
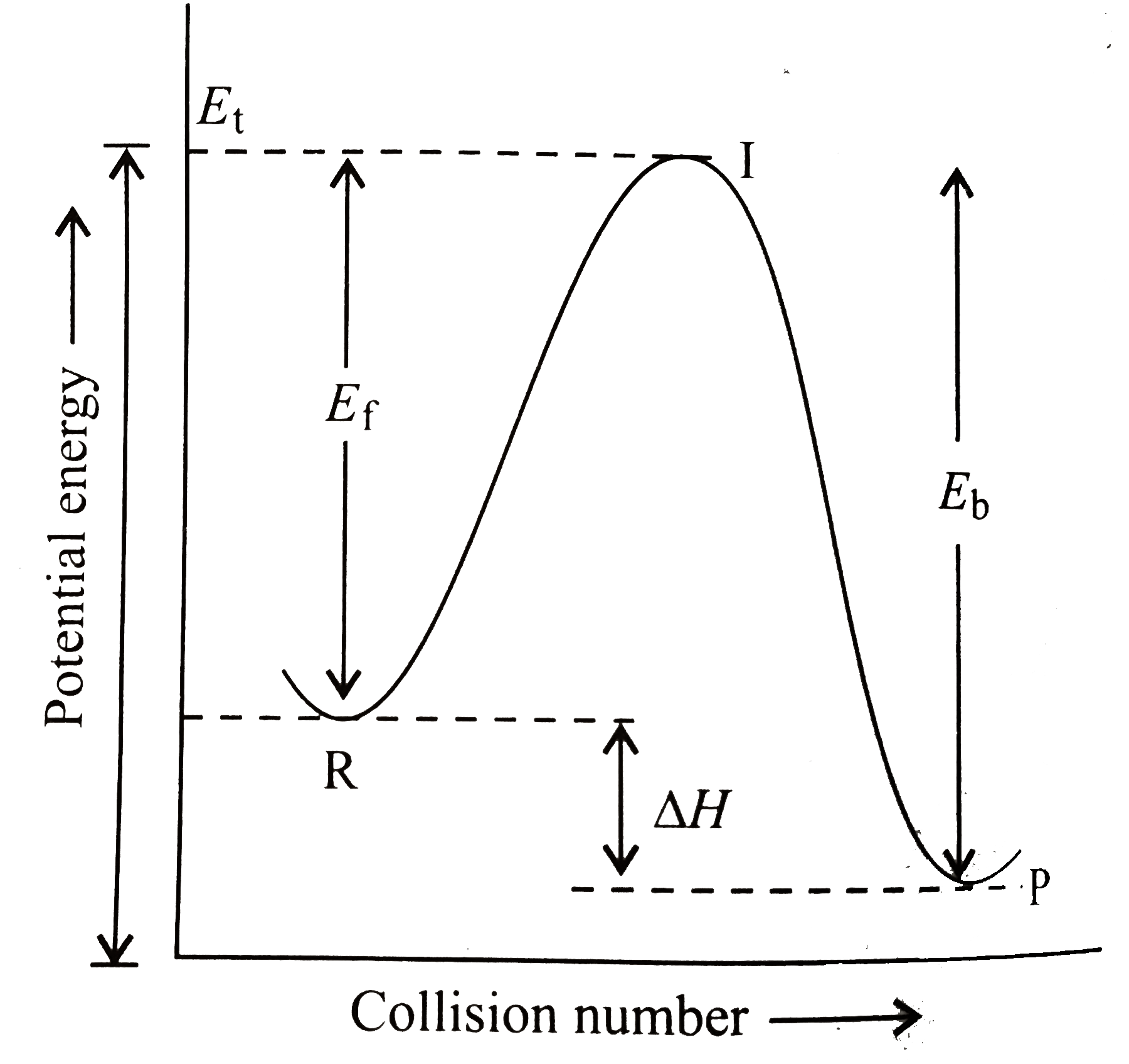
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The activation eneries for forward and backward reactions in a chemical reaction are 30.5 and 45.4kJmol−1 respectively. The reaction is
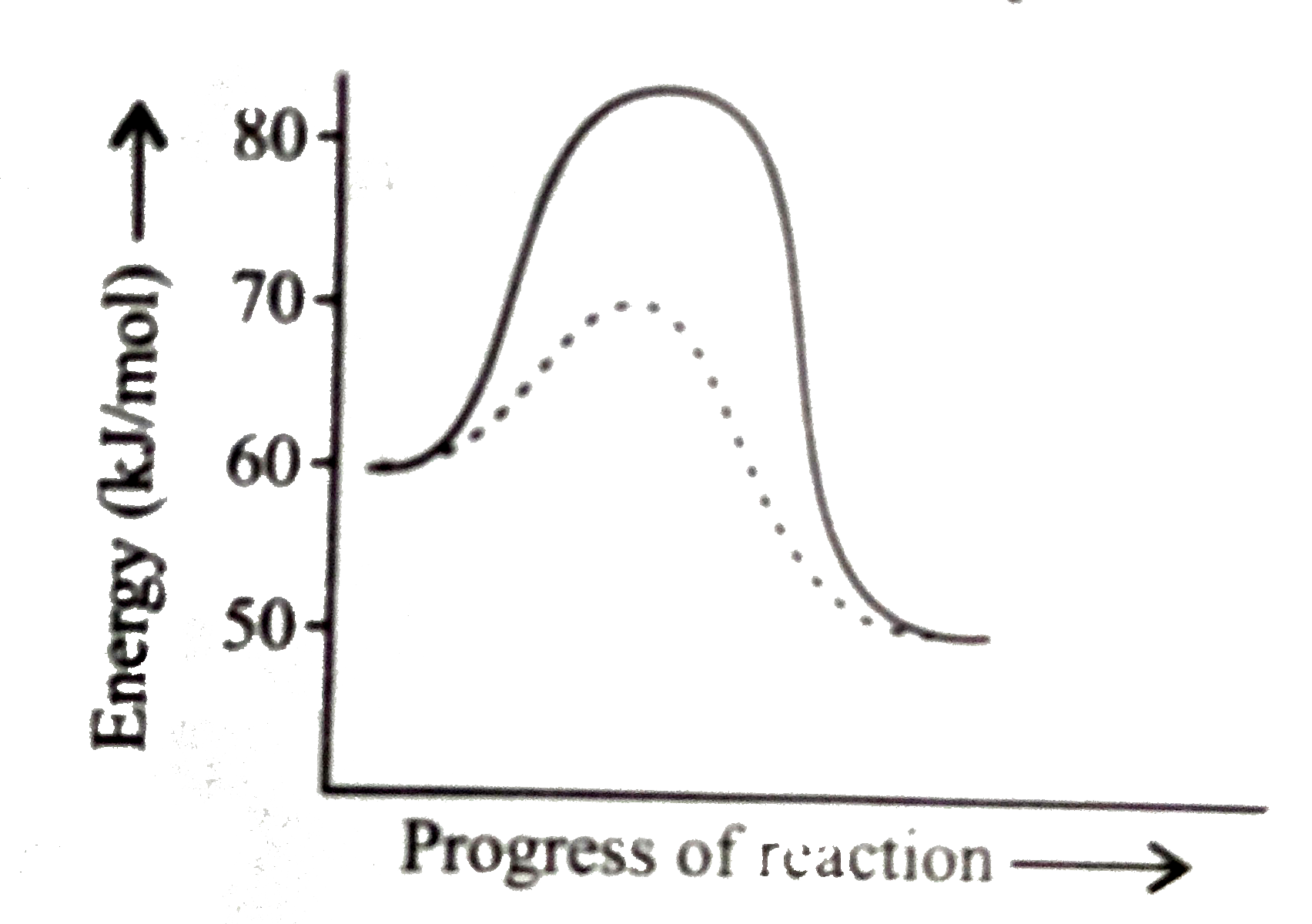
View SolutionFor a reaction A2+B2⇔2AB the figure shows the path of the reaction in absence and presence of a catalyst. What will be energy of activation for forward (Ef) and backward (Eb) reaction in presence of a catalyst and ΔH for the reaction? The dotted curve is path of reaction in presence of a catalyst.
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1. Calculate Energy of activation for forward and backward reaction (EfandEa) at 300 K. Given that EfandEb are in the ratio 20 : 31. Assume that pre-exponential factor is same for forward and backward reaction.
View SolutionThe energy of activation is lowest for which reaction?
View SolutionThe activation energies of the forward and backward reactions in the case of a chemical reaction are 30.5 and 45.4kJ/mol respectively. The reaction is:
View SolutionThe activation energies of the forward and backward reactions in the case of a chemical reaction are 37.5 and 51.3 kJ/mole respectively The reaction is
View SolutionIf Ef and Er are the activation energies of forward and backward reactions and the reaction is known to be exothermic, then
View SolutionIf the activation energies of the forward and backward reactions of a reversible reaction are Ea(f) and Ea(b), respectively. The ΔE of the reaction is ………..
View SolutionThe activation energies for forward and backward reactions are EfandEb respectively. If the reaction is exothermic then which is true regarding relation of activation energies?
View Solution
