Establish a relationship between ΔH and ΔU in Haber synthesis of ammonia assuming that gaseous reactants and products are ideal.
To establish the relationship between ΔH (change in enthalpy) and ΔU (change in internal energy) in the Haber synthesis of ammonia, we can follow these steps:
Step 1: Write the balanced chemical equation for the Haber process.
The balanced equation for the synthesis of ammonia (NH₃) from nitrogen (N₂) and hydrogen (H₂) is:
N2(g)+3H2(g)→2NH3(g)
Step 2: Identify the change in moles of gas (Δn).
To find Δn, we need to calculate the difference between the moles of gaseous products and the moles of gaseous reactants.
- Moles of gaseous products (NH₃): 2
- Moles of gaseous reactants (N₂ + 3H₂): 1 + 3 = 4
Thus,
Δn=moles of products−moles of reactants=2−4=−2
Step 3: Use the relationship between ΔH and ΔU.
The relationship between change in enthalpy (ΔH) and change in internal energy (ΔU) is given by the equation:
ΔH=ΔU+Δ(P⋅V)
For ideal gases, we can express Δ(PV) as ΔnRT, where R is the gas constant and T is the temperature.
Step 4: Substitute Δ(PV) with ΔnRT.
From the previous step, we substitute Δ(PV) with ΔnRT:
ΔH=ΔU+ΔnRT
Step 5: Substitute the value of Δn.
Now, substituting the value of Δn we calculated:
ΔH=ΔU+(−2)RT
This simplifies to:
ΔH=ΔU−2RT
Conclusion:
Thus, the relationship between ΔH and ΔU for the Haber synthesis of ammonia is:
ΔH=ΔU−2RT
The balanced equation for the synthesis of ammonia (NH₃) from nitrogen (N₂) and hydrogen (H₂) is:
N2(g)+3H2(g)→2NH3(g)
To find Δn, we need to calculate the difference between the moles of gaseous products and the moles of gaseous reactants.
- Moles of gaseous reactants (N₂ + 3H₂): 1 + 3 = 4
Δn=moles of products−moles of reactants=2−4=−2
The relationship between change in enthalpy (ΔH) and change in internal energy (ΔU) is given by the equation:
ΔH=ΔU+Δ(P⋅V)
For ideal gases, we can express Δ(PV) as ΔnRT, where R is the gas constant and T is the temperature.
From the previous step, we substitute Δ(PV) with ΔnRT:
ΔH=ΔU+ΔnRT
Now, substituting the value of Δn we calculated:
ΔH=ΔU+(−2)RT
This simplifies to:
ΔH=ΔU−2RT
Thus, the relationship between ΔH and ΔU for the Haber synthesis of ammonia is:
ΔH=ΔU−2RT
Topper's Solved these Questions
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Conceptual Questions - 2
17 Videos
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Conceptual Questions - 3
18 Videos
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Advanced Level Problems
15 Videos
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Unit Practice Test
13 Videos
Similar Questions
Knowledge Check
The relation between ΔU and ΔH:
AΔH=ΔU−PΔVBΔH=ΔU+PΔVCΔH=ΔV+ΔHDΔU=ΔH+PΔV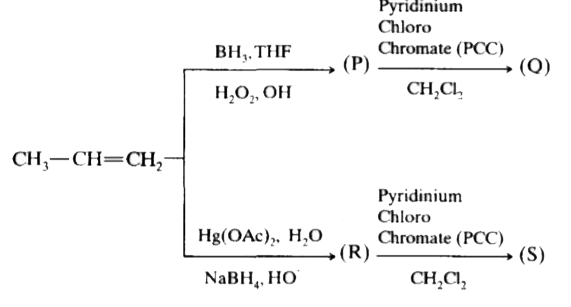
Relationship between products (Q) and (S) isApositional isomerBchain isomer.Cstereoisomer.Dfunctional isomer.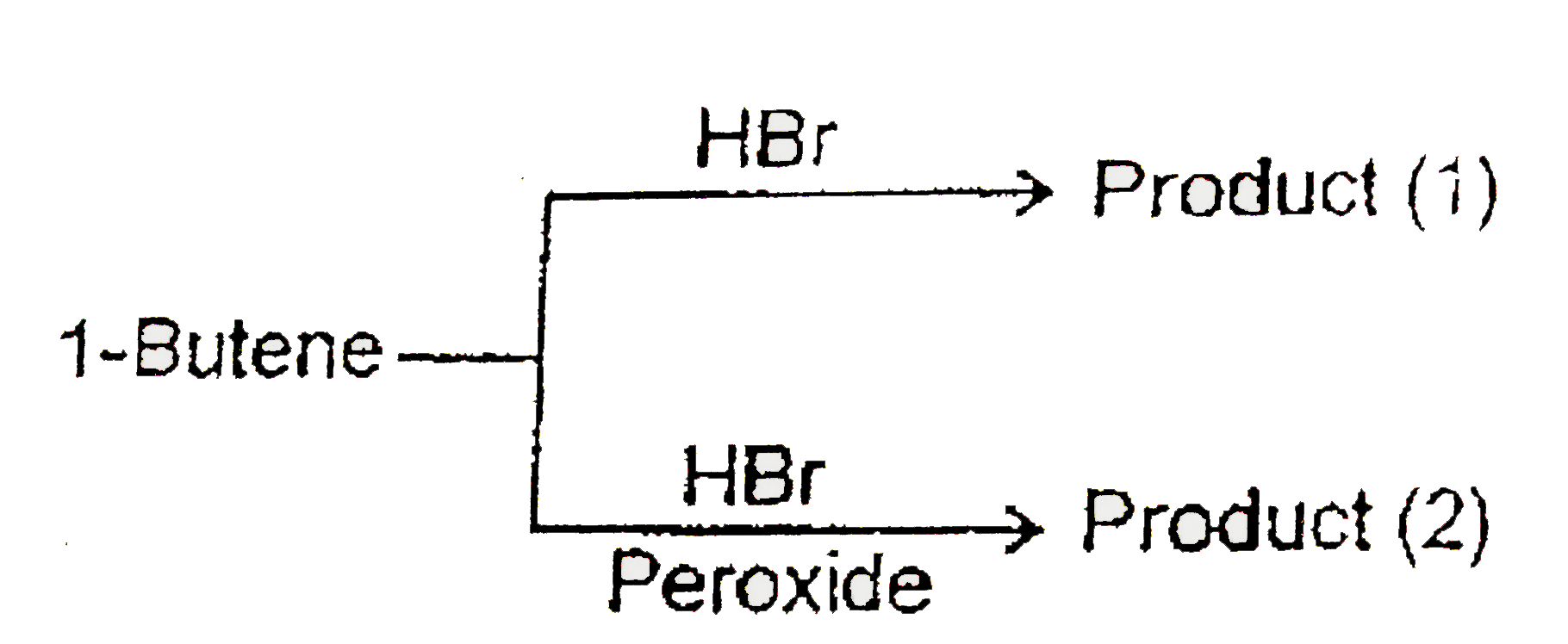
Relationship between product 1 and 2 is :APositional isomerBFunctional group isomersCChain isomerDMetamer
Name the law which deals with the ratios of the volumes of the gaseous reactants and products.
View SolutionDerive a relationship between Kb,Tb and ΔHvap for a liquid.
View SolutionWhat is the relationship between marginal product and marginal cost?
View Solution
Relationship between products (Q) and (S) is :
View Solution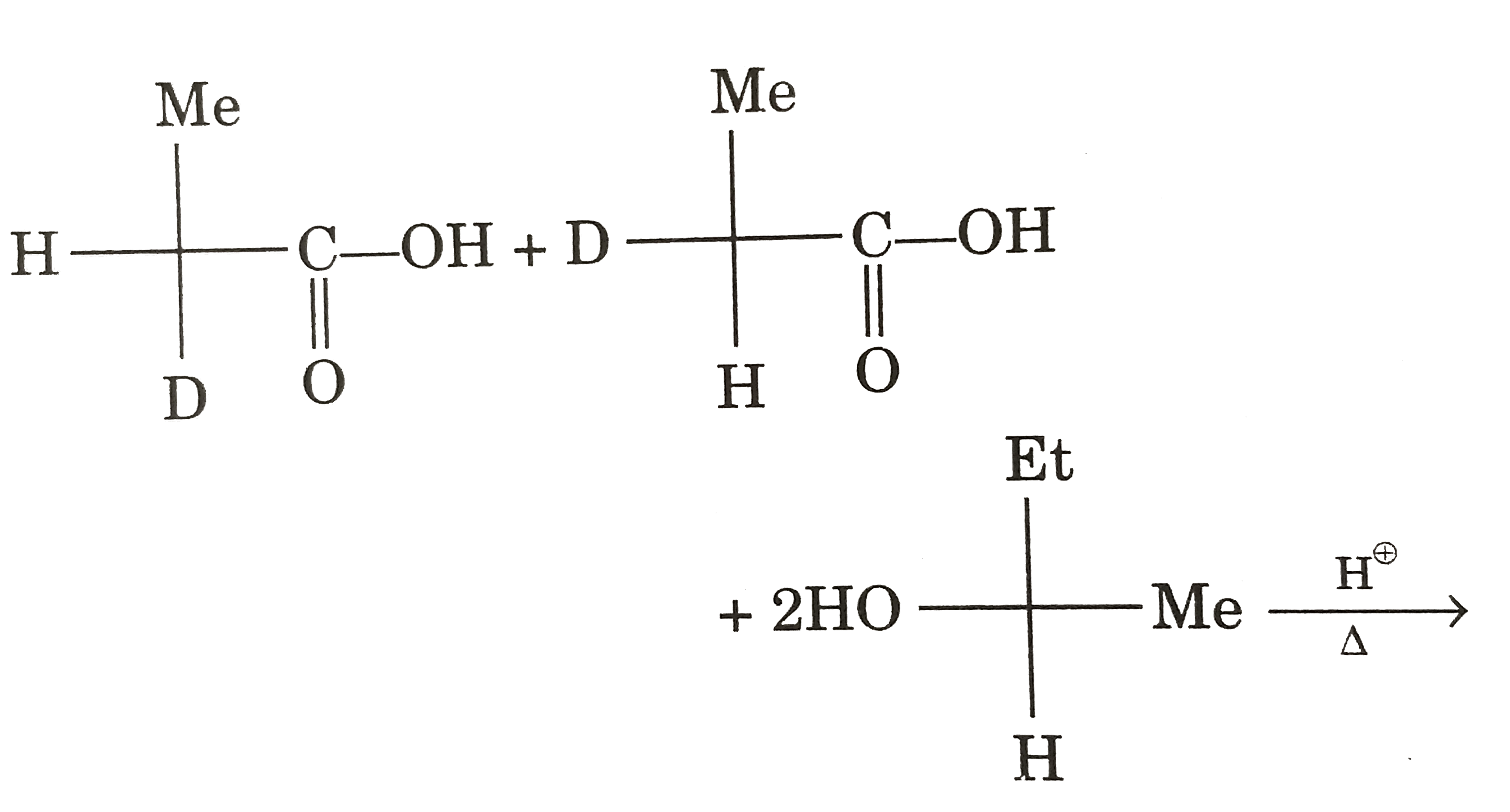
Relationship between formed products is :
View Solution
