Experimentally it was found that a metal oxide in formula M0.98O. Metal M is present as M2+ and M3+ in its oxide ,Fraction of the metal which exists as M3+ would be
4.08%
6.05%
5.08%
7.01%
The correct Answer is:1
To solve the problem, we need to determine the fraction of the metal M that exists in the M3+ oxidation state in the metal oxide M0.98O. Here’s a step-by-step breakdown of the solution:
Step 1: Define the variables
Let:
- x = number of moles of M3+
- 98−x = number of moles of M2+
Step 2: Write the charge balance equation
The total charge contributed by the metal ions and oxygen must equal zero for the compound to be electrically neutral. The charge from oxygen (which is always −2) for 100 moles of the oxide is:
Total charge from oxygen=−2×100=−200
The charge contributed by M3+ and M2+ can be expressed as:
Total charge from metal=3x+2(98−x)
Step 3: Set up the equation for charge neutrality
Setting the total charge from the metal equal to the total charge from oxygen gives us:
3x+2(98−x)−200=0
Step 4: Simplify the equation
Expanding and simplifying the equation:
3x+196−2x−200=0
x−4=0
x=4
Step 5: Calculate the fraction of M3+
Now that we have x=4, we can find the fraction of M3+ in the total amount of metal:
Total amount of metal=0.98 moles
The fraction of M3+ is:
Fraction of M3+=x0.98=40.98
Step 6: Calculate the percentage
To find the percentage of M3+:
Percentage of M3+=(40.98)×100≈4.08%
Final Answer
The fraction of metal M that exists as M3+ is approximately 4.08%.
---
Let:
- x = number of moles of M3+
- 98−x = number of moles of M2+
The total charge contributed by the metal ions and oxygen must equal zero for the compound to be electrically neutral. The charge from oxygen (which is always −2) for 100 moles of the oxide is:
Total charge from oxygen=−2×100=−200
Total charge from metal=3x+2(98−x)
Setting the total charge from the metal equal to the total charge from oxygen gives us:
3x+2(98−x)−200=0
Expanding and simplifying the equation:
3x+196−2x−200=0
x−4=0
x=4
Now that we have x=4, we can find the fraction of M3+ in the total amount of metal:
Total amount of metal=0.98 moles
The fraction of M3+ is:
Fraction of M3+=x0.98=40.98
To find the percentage of M3+:
Percentage of M3+=(40.98)×100≈4.08%
The fraction of metal M that exists as M3+ is approximately 4.08%.
Topper's Solved these Questions
- SOLID STATEBOOK - R SHARMACHAPTER - SOLID STATEEXERCISE - Archives
28 Videos
- SOLID STATEBOOK - R SHARMACHAPTER - SOLID STATEEXERCISE - QUESTION BANK level 1
4 Videos
- POLYMERSBOOK - R SHARMACHAPTER - POLYMERSEXERCISE - All Questions
65 Videos
- SOLUTIONSBOOK - R SHARMACHAPTER - SOLUTIONSEXERCISE - ARCHIVES
42 Videos
Similar Questions
Knowledge Check
Experimentally it was found that a metal oxide has formula M0.98O. Metal M is presented as M2+andM3+ in its oxide. Fraction of the metal which exists as M3+ would be
A5.08%B7.01%C4.08%D6.05%Experimentally it was found that a metal oxide has formula M0.98O. Metal M is present as M2+andM3+ in iyts oxide. Fraction of the metal which exists as M3+ would be
A0.0508B0.0701C0.0408D0.0605Experimentally it was found that a metal oxide has formula M0.98O. Metal M present as M2+ and M3+ in its oxide. Fraction of the metal which exists as M3+ would be:
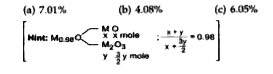 A5.08%B7.01%C4.08%D6.05%
A5.08%B7.01%C4.08%D6.05%
Analysis shows that a metal oxide has the empirical formula M0.96O1.00. Calculate the percentage of M2+ and M3+ ions in the sample.
View SolutionExperimentally it was found that a metal oxide has formula M0.98O. Metal M present as M2+ and M3+ in its oxide. Fraction of the metal which exists as M3+ would be:
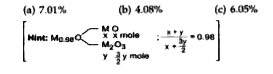
View SolutionExperimentally it was found that a metal oxide has formula M0.98, Metal M, is present as M+2 and M+3 in its oxid. Fraction of the metal which exist as M_(+3) would be :
View SolutionExperimentally it was found that a metal oxide has dormula M0.98O. Metal M, present as M2+andM3+ in its oxide. Fraction of the metal which exist as M3+andM3+ in its oxide. Fraction of the metal which exists as M3+ would be:
View SolutionExperimentally it is was found that a metal oxide has formula M0.95O .Metal M present as M3+ in its oxide fraction of the metal which exits as M2+ would be
View Solution
