Explain AAAA and ABABA and ABCABC type of three dimensional packing with the help of neat diagram.
(i) AAAA type of three dimensional packing:
This type of three dimensional packing arrangements can be obtained by repeating the AAAA type two dimensional arrangements in three dimensions. i.e., spheres in one layer sitting directly on the top of those in the previous layer so that all layers are identical. All spheres of different layers of crystal are perfectly aligned horizontally and also vertically, so that any unit cell of such arrangement as simple cubic structure as shown in fig.
In simple cubic packing, each sphere is in contact with 6 neighbouring spheres - Four in its own layer, one above and one below and hence the coordination number of the sphere in simple cubic arrangement is 6.

(ii) ABABA type of three dimensional packing:
In this arrangement, the spheres in the first layer (A type) are slightly separated and the second layer is formed by arranging the spheres in the depressions between the spheres in layer A as shown in figure. The third layer is a repeat of the first. This pattern ABABAB is repeated throughout the crystal. In this arrangement, each sphere has a coordination number of 8, four neighbors in the layer above and four in the layer below.

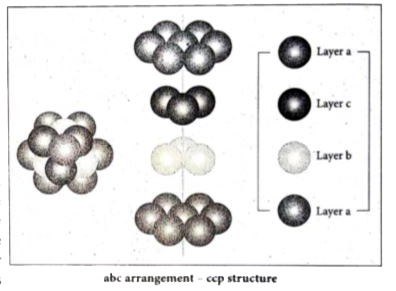
(iii) ABCABC type of three dimensional packing:
In this arrangement (FCC) second layer spheres are arranged at the dips of the first layer. Third layer spheres are arranged in a manner such that it cover the octahedral void. Then no longer third layer is similar to first or second layer. Third layer gives different arrangement. Fourth layer spheres are similar to first layer. If the first, second and third layer are represented as A, B, C then this type of packing gives the arrangement of layers as ABCABC... (i.e.,), the first three layers do not resemble first, second and third layers respectively and the sequence is repeated with the addition of more layers.
In this arrangement atoms occupy 74% of the available space and thus has 26% vacant space. The coordination number is 12.
Voids : The empty spaces between the three dimensional layers are known as voids. There are two types of common voids possible. They are tetrahedral and octahedral voids.
Tetrahedral void:
A void formed by three spheres of a layer in contact with each other and also with a sphere on the top or bottom layer is a hole between four spheres. The spheres are arranged at the vertices of a regular tetrahedron such a hole or void is called tetrahedral void.
Octahedral void:
A hole or void formed by three spheres of a hexagonal layer and another three spheres of the adjacent layer is a hole between six spheres. The spheres are arranged at the vertices of a regular octahedron. Such a hole or void is called octahedral void.
Topper's Solved these Questions
- SAMPLE PAPER - 7 (SOLVED) BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 7 (SOLVED) EXERCISE - PART-III
9 Videos
- SAMPLE PAPER - 6 (SOLVED) BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 6 (SOLVED) EXERCISE - PART IV
10 Videos
- SAMPLE PAPER - 9 (SOLVED)BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 9 (SOLVED)EXERCISE - PART-IV
10 Videos
Similar Questions
Describe the mechanism of translation with the help of neat and labelled diagram.
View SolutionExplain oogenesis with the help of a neat labelled diagram
View SolutionExplain the structure of root hair with the help of neat and labelled diagrams.
View SolutionExplain reflection of light at a plane surface with the help of a neat ray diagram.
View SolutionExplain partial reflection, critical angle and total internal reflection with the help of a neat labelled diagram.
View SolutionExplain processing of hn-RNA with the help of neat and labelled diagram.
View SolutionWhat are esters? Explain the preparation of ethyl ethanoate with the help of neat labelled diagram.
View SolutionWhat are esters? Explain the preparation of ethyl ethanoate with the help of neat labelled diagram.
View SolutionExplain magnetic separation process of ores with the help of a neat , labelled diagram.
View SolutionExplain Miller and Urey experiment with the help of a neat and labelled diagram. Also write its results and conclusions
View Solution
