Question

Explain optical isomerism or Geometrical isomerism with example.

Explanation

(a) Geometrical isomerism : The restricted rotation of atoms or groups around the doubly bended carbon atoms gives rise to different geometries of such compounds. The stereoisomers of these types are called stereoisomers. E.g., Cis and trans isomers have different geometry therefore, they are geometrical isomers.
(b) Geometrical isomers and isomerism : In alkene, there is group attached to carbon (1) and carbon (2) attached to it have YXC = CXY different geometry are of two types.

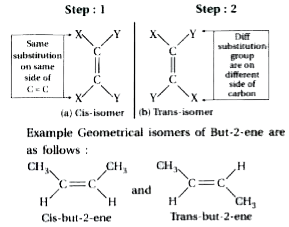
Cis-isomer : In which two identical atoms or groups lie on the same side of the double bond is called cis isomers.
Trans-isomers : In which identical atoms or groups lie on the opposite sides of the double bond is called trans isomers.
Cis and Trans isomer : Groups or molecules arranged in different geometry known as geometrical isomers.
Due to the arrangement reaction for the Cis and Trans isomers : YXC = CXY has two different structure a and b, then at the group C=C, their is no rotation of groups there is restricted rotation on around C=C therefore, there are different arrangement on the C=C bond. Therefore they are geometrical isomers.
ON rotation of molecule a and b `180^(@)`, C=C bond should be broken, due to which `a harr b` do not convert each other, therefore they are different isomers.
Different geometry : Due to different arrangement of atoms or groups in space, these isomer differ in their properties like melting point, boiling point, dipole moment, solubility etc. XYC = CXY or XYC = CXZ and XYC = CZW alkene has different geometrical structures.
(i) Alkene XYC = CXY e.g. : HCl = CHCl
(ii) Alkene XYC = CZW e.g. : CHCl = C Cl Br
(iii) Alkene XYC = CXZ e.g. : CHCl = CHBr
Here possibilities of geometrical isomers.
Cis and trans are two geometrical isomers.
Cis and trans are two geometrical isomers, in which cis are on the same side atoms or groups substituted and trans they are on opposite side.
In cis and trans, there is restricted rotation around C=C. Rotation is only possible on breaking the bond between C=C.