Explain the dual behaviour of matter. Discuss its significance to microscopic particles like electrons. Solution in Telugu
de - Broglie's hypothesis :The light is found to exhibit wave nature as well as particle nature (dual nature ) . Based on this idea of ' duel nature of light '. De Broglie in 1924 proposed that " all micro -particles including the electron moving with high velcoity are as sociated with dual nature (i.e., ) both particle wave nature .
De- broglie an expression for the wavelength of the moving electron .
Expression for de-Broglie wavelengths :
According to 'Planck's quantum theory' , energy of a photon ,
E=hυ, But υ=cλ
∴E=h.cλ......(1)
Einstein's mass - energy equivalence equation is E=mc2 .......(2)
combining eqns. (1) and (2) ,
h.cλ=mc2 or λ=hmc=hp
(p=mc=momentum)
This equations is applicable to photons as well as to all microparticles , moving with high speed .
∴ We can write in general, λ=hp=hmv
where m = mass of the microparticle and v = its velocity
λ , is called , de-Broglie wavelength or material wavelength .
Significance of de - Broglie's concept:
According to Bohr's theory , electron revolves in an orbit in which its angular momentum (mvr) is an integral multiple of h2π . Bohr assumed electron as a particle .
Hence his equation can be taken as mvr=n(h2π) where n = a whole number .
According de Broglie , electron behaves as a standing (or stationary ) wave which extends round the nucleus in a circular orbit . If the ends of the electron wave meet to give a regular series of crests and troughs , the electron - wave is said to be 'in phase' . It means , there is constructive interfernce of electron waves and the electron motion has a character of standing wave or non-energy radiating motion . Always it is a necessary condition motion . Always it is a necessary condition to get an electron-wave in phase'such that the circumference fo the Bohr's orbit (=2πr) is equal to the whole number of multiple of the wavelength (λ) of the electron -wave .
nλ=2πr
λ=2πrn
But λ=hmv (de-Broglie)
∴2πrn=hmv or mvr=nh2π
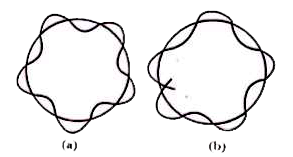
(a) Wave in - phase (b) Wave out -of phase
This is Bohr's equation which stipulates that "the angular momentum of an electron moving round the nuclecus is an integral multiple of h2π" . This shows that, de-Broglie's theory and Bohr's theory are in agreement with each other .
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ATOMIC STRUCTUREEXERCISE - ADDITIONAL QUESTIONS & ANSWERS
22 Videos
- ATOMIC STRUCTUREBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ATOMIC STRUCTUREEXERCISE - SHORT ANSWER QUESTIONS
18 Videos
- AP MARCH-2018 I.P.E. PAPERBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - AP MARCH-2018 I.P.E. PAPEREXERCISE - SECTION-C
5 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - LONG ANSWER QUESTIONS
9 Videos
Similar Questions
Calculate the number of protons , neutrons and electrons in .8035Br
View SolutionWhat is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 5 to an energy level with n = 3 ?
View SolutionWhat are the postulates of Bohr's model of hydrogen atom ? Discuss the importance of this model to explain various series of line spectra in hydrogen atom.
View SolutionExplain the formation of Ionic Bond with a suitable example.
View SolutionDual behaviour of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other types of material. If the velocity of the electron in this microscope is 1.6 xx 10^(6) ms^(-1) , calculate de Broglie wavelength associated with this electron.
View SolutionDual behaviour of matter proposed by de Broglie the discovery of electron microscope often used for the highly magnified images of biological molecules and other types of material. If the velocity of the electron in this microscope is 1.6xx10^(6)m*s^(-1) , calculate de Broglie wavelength associated with this electron.
View SolutionWhat are the evidence in favour of dual behaviour of electron?
View SolutionThe dual nature of matter imposes a limitation on the simultaneous determination of ________ and ___________ of a microscopic particle.
View Solutionపదార్థం ద్వంద్వ స్వభావాన్ని వివరించండి. ఎలక్ట్రాన్ లాంటి సూక్ష్మ కణాలకు దీని ప్రాముఖ్యాన్ని చర్చించండి.
View SolutionDual behaviour of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is 1.6xx10^(6) m s^(-1) . Calculate de Broglie wavelength associated with this electron.
View SolutionExplain particle-wave (dual) nature of matter.
View SolutionThe dual behaviour of matter was proposed by the French physicist , de Broglie.
a) State the dual behaviour of matter.
View SolutionThe dual behaviour of matter was proposed by the French physicist, de Broglie. State the dual behaviour of matter.
View SolutionExplain dual nature of matter and radiation.
View SolutionDual behaviour of matter proposed by de-Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of electron in this microscope is 1.6×106ms−1. calculate de-Broglie wavelength associated with this electron.
View Solution
