For 1=3, which value of m is not possible?
4
0
−3
−1
The correct Answer is:A
To determine which value of m is not possible when l=3, we need to understand the relationship between the azimuthal quantum number l and the magnetic quantum number m.
1. Understanding Quantum Numbers:
- The azimuthal quantum number l can take on integer values starting from 0 up to n−1, where n is the principal quantum number.
- The magnetic quantum number m can take values from −l to +l.
2. Given Value of l:
- In this case, we have l=3.
3. Determining Possible Values of m:
- The possible values of m when l=3 are:
m=−l,−l+1,…,0,…,l−1,l
- This translates to:
m=−3,−2,−1,0,1,2,3
4. Counting the Values:
- The total values of m are:
- −3
- −2
- −1
- 0
- 1
- 2
- 3
- This gives us a total of 7 possible values.
5. Identifying the Not Possible Value:
- Since m can only take values from −3 to 3, any value outside this range is not possible.
- For example, m=4 is not a valid value for l=3.
Conclusion:
The value of m that is not possible when l=3 is 4.
- The azimuthal quantum number l can take on integer values starting from 0 up to n−1, where n is the principal quantum number.
- The magnetic quantum number m can take values from −l to +l.
- In this case, we have l=3.
- The possible values of m when l=3 are:
m=−l,−l+1,…,0,…,l−1,l
- This translates to:
m=−3,−2,−1,0,1,2,3
- The total values of m are:
- −3
- −2
- −1
- 0
- 1
- 2
- 3
- This gives us a total of 7 possible values.
- Since m can only take values from −3 to 3, any value outside this range is not possible.
- For example, m=4 is not a valid value for l=3.
The value of m that is not possible when l=3 is 4.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
m=- 1 is not possible for :
A3px orbitalB4dx2−y2 orbitalC2s orbitalD4f orbital - Question 2 - Select One
If 5x≡2 (mod 3), then which of the following is a possible value of x?
A3B315C0DNone of these - Question 3 - Select One
If 7x≡1 (mod 5),then which of the following is a possible value of x?
A10B11C12DNone of these
If the equation x2−(2k+1)x+k+2=0 has exactly one root in (0, 2) such that maximum possible negative integral value of k is m and minimum possible positive integral value of k is M, then IM – m| is
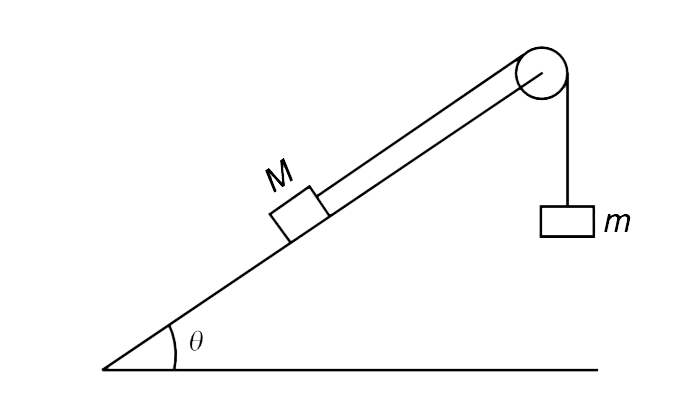
View SolutionA particle of mass M rests on a rough inclined plane at an angle q to the horizontal(sinθ=45). It is connected to another mass m as shown in fig. The pulley and string are light. The largest value of m for which equilibrium is possible is M. Find the smallest value of m for which equilibrium is possible
 View Solution
View SolutionWhat is the value of (n+l+m2) for all possible orbitals with number of radial nodes = 1 and where n≤3.
View Solution(a) If the quantum number 'l' has value of 2, what are permitted values of the quantum number ml ?
(b) An atomic orbital has n = 3, what are the possible values of l ?
(c ) An atomic orbital has l = 3, what are the possible values of ml ?View SolutionAssertion : For l = 2, ml can be -2, -1, 0, +1 and +2.
Reason : For a given value of l, (2l + 1) values of ml are possible.View Solution

