For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)
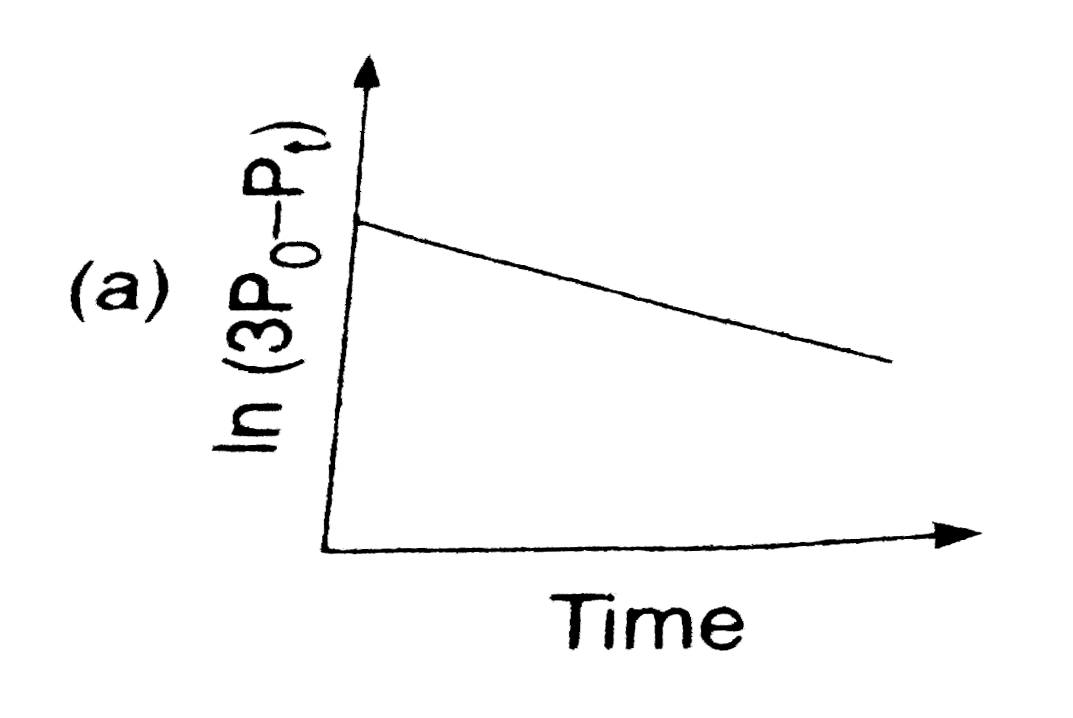
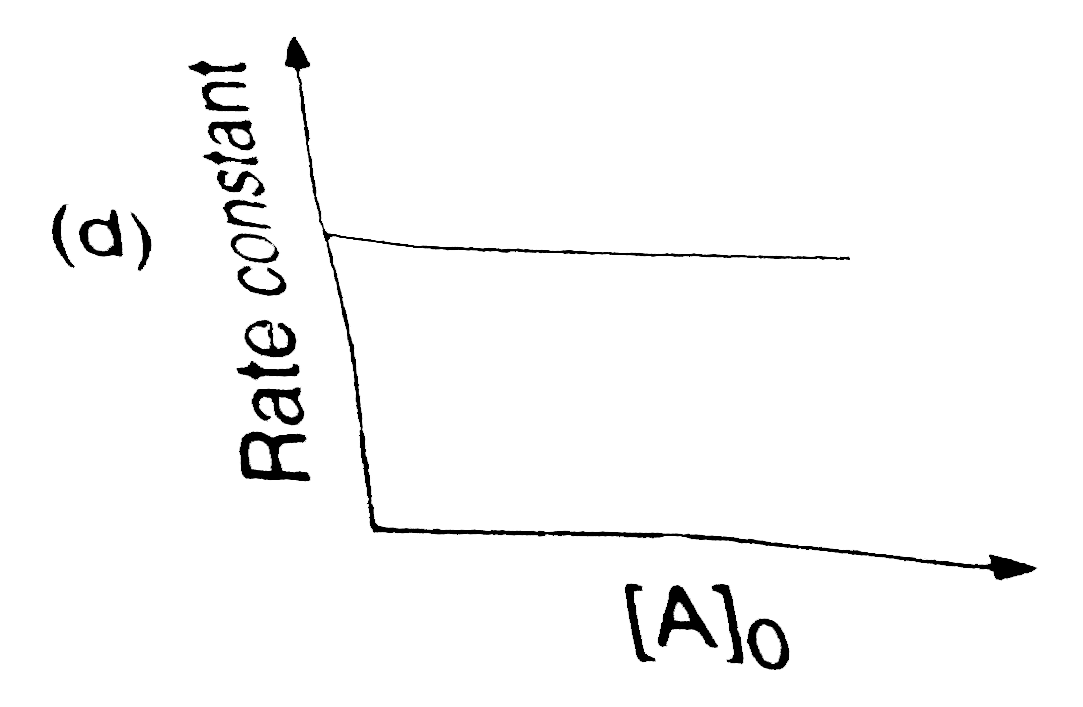
The correct Answer is:A, D
The given reaction is:
A(g)→2B(g)+C(g)
Initiallyt0p000After time 't'p0−x2xx
a∝p0
pt=p0−x+2x+x
=p0+2x
x=12(p1p0)
(a−x)∝p0−12(pt−p0)
∝(3p0−pt)2
For first order reaction :
k=1tln(aa−x)
=1tln.p0(3p0−pt)/2
=1tln.2p0(3p0−pt)
kt=ln2p0−ln(3p0−pt)
ln(3p0−pt)=ln2p0−kt .....(i)
Y=C+mx
Equation (i) represnts straight line with negative slope hence graph (a) is correct. Rate constant does not depend on the concentration of reactant hence does not depend on the concntration of reactant hence graph (d) is also correct.
Topper's Solved these Questions
- BOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - ASSERTION- REASON TYPE QUESTIONS14videos
CHEMICAL KINETICS
- BOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - MATRIX MATCHING TYPE QUESTIONS11videos
CHEMICAL KINETICS
- BOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - OBJECTIVE QUESTIONS (LEVEL-B) SET I48videos
CHEMICAL KINETICS
- BOOK - OP TANDONCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Integer4videos
CARBOXYLIC ACIDS AND THEIR DERIVATIVES
- BOOK - OP TANDONCHAPTER - Chemical Thermodynamics and ThermochemistryEXERCISE - Self Assessment (Integer type).3videos
Chemical Thermodynamics and Thermochemistry
Similar Questions
For a gas phase first order reaction,
A(g)→B(g)+2C(g)+D(g)
The initial pressure was P0 While pressure after 't' time becomes Pt (Pt>P0). The expression for the rate constant (K) would beView SolutionConsider a first order reaction at "450K
X(g)→Y(g)+Z(g)
What is the rate constant of the reaction using given data? [Assume initially only X is present ]
[Time(s)05( Total Pressure )1520]View Solution
Knowledge Check
- Question 1 - Select One or More
For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t and P0 and Pt respectively, Initially, only A is present with concentration [A]0 and t1/3 is the required for the partial pressure of A to reach 1/3rd of its initial value. The correct option(s) is are
(Assume that all these gases behave as ideal gases)A B
B C
C D
D
- Question 2 - Select One
For a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)A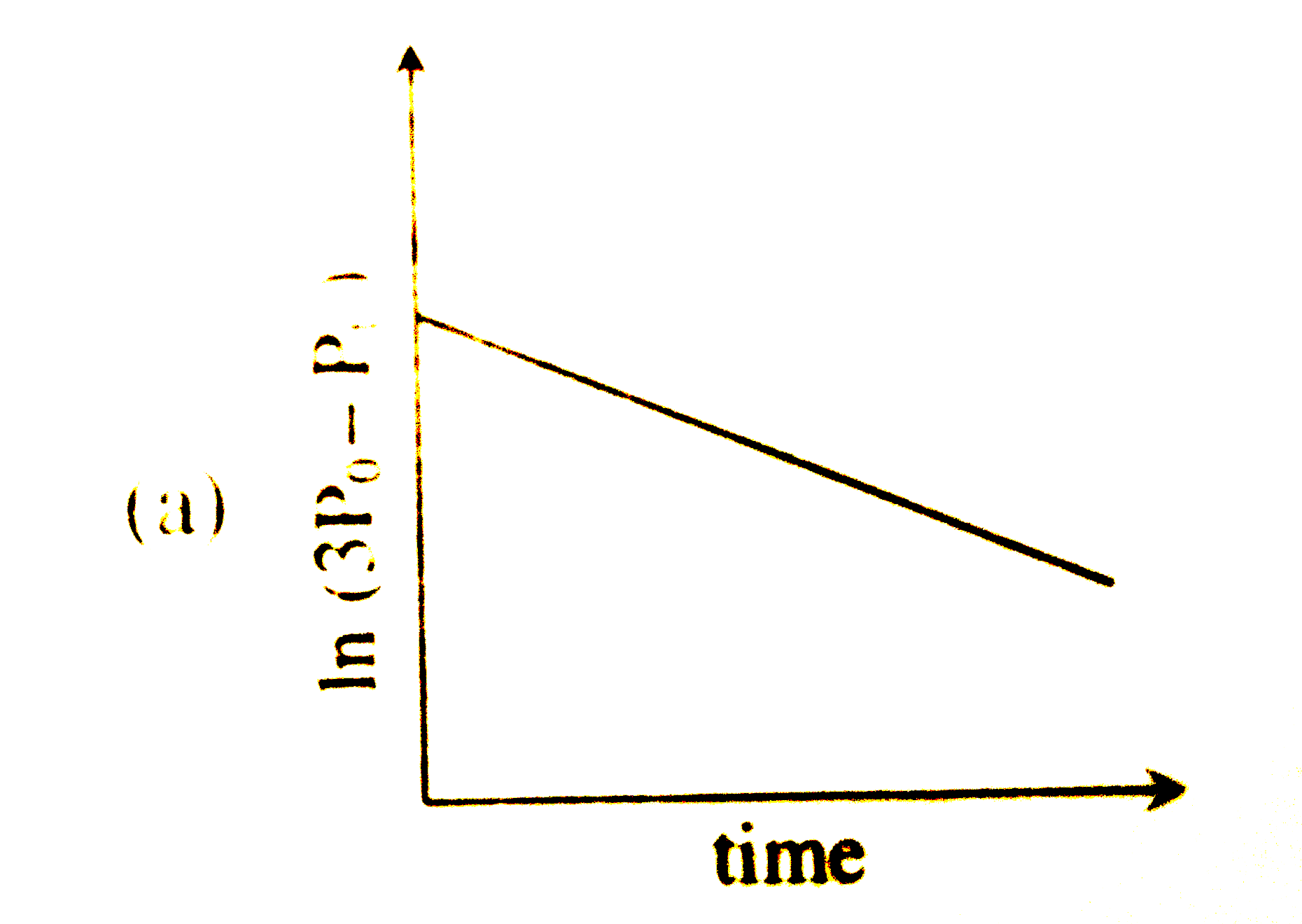 B
B C
C D
D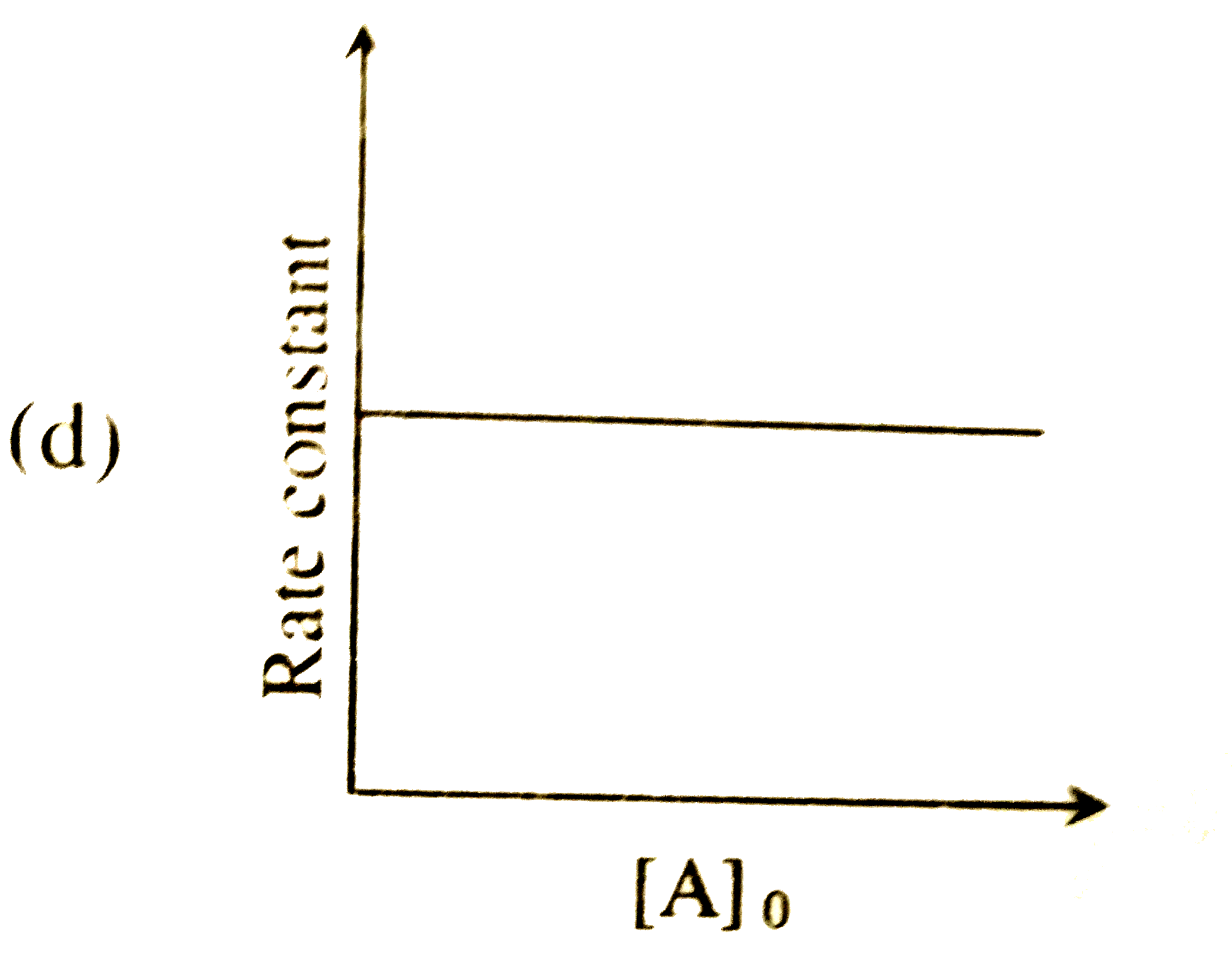
- Question 3 - Select One
For a first order gas phase reaction :
A(g)→2B(g)+C(g)
P0 be initial pressure of A and Pt the total pressure at time 't'. Integrated rate equation is :A2.303tlog(P0P0−Pt)B2.303tlog(2P03P0−Pt)C2.303tlog(P02P0−Pt)D2.303tlog(2P02P0−Pt)
For the first order reaction A(g)→2B(g)+C(g), the initial pressure is PA=90 mm Hg, the pressure after 10 minutes is found to be 180 mm Hg. The rate constant of the reaction is
View SolutionFor the first order gas phase decomposition reaction,
A(g)→B(g)+C(g)
if P0 is the initial pressure of A and Pt is total pressure after time t, thenView SolutionFor a first order reaction :
A(g) → B(g) + C(g)+ D(g)
Occurring at 1 bar pressure and 300 K if initial volume of the container containing only A is V0 and after 10 minutes it is V10 then average life of A will be (in minutes) :View SolutionIn a first-order reaction of the type: A(g)→2B(g), the initial and final pressures are P1 and p respectively. The rate constant can be expressed by
View SolutionFor a first order reaction R→P, the rate constant is k. if the initial concentration of R is [R0], the concentration of R at any time 't' is given by the expression-
View Solution
