For an isothermal reversible expansion process, the value of q can be calculated by the expressin
q=2.303nRTlog.V2V1
q=−2.303nRTlog.V2V1
q=−2.303nRTlog.V1V2
q=−PexpnRTlog.V1V2
The correct Answer is:A
To solve the problem regarding the calculation of q for an isothermal reversible expansion process, we can follow these steps:
1. Understand the Isothermal Process:
- An isothermal process is one where the temperature (T) of the system remains constant throughout the process. Therefore, the change in temperature (ΔT) is equal to 0.
2. Apply the First Law of Thermodynamics:
- The first law of thermodynamics states that:
ΔU=Q+W
- Where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
3. Determine Change in Internal Energy:
- For an ideal gas, the change in internal energy (ΔU) can be expressed as:
ΔU=nCVΔT
- Since ΔT=0 for an isothermal process, it follows that:
ΔU=0
4. Relate Heat and Work:
- From the first law of thermodynamics, substituting ΔU=0:
0=Q+W⟹Q=−W
5. Calculate Work Done (W):
- The work done during an isothermal expansion of an ideal gas can be calculated using the formula:
W=−nRTln(V2V1)
- Here, n is the number of moles, R is the universal gas constant, T is the absolute temperature, V2 is the final volume, and V1 is the initial volume.
6. Substitute Work into the Heat Equation:
- Now substituting the expression for W into the equation for Q:
Q=−(−nRTln(V2V1))=nRTln(V2V1)
7. Final Expression for Q:
- Thus, we can express Q as:
Q=nRTln(V2V1)
8. Check Options:
- Finally, check the provided options to find the one that matches this derived expression for Q.
- An isothermal process is one where the temperature (T) of the system remains constant throughout the process. Therefore, the change in temperature (ΔT) is equal to 0.
- The first law of thermodynamics states that:
ΔU=Q+W
- Where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
- For an ideal gas, the change in internal energy (ΔU) can be expressed as:
ΔU=nCVΔT
- Since ΔT=0 for an isothermal process, it follows that:
ΔU=0
- From the first law of thermodynamics, substituting ΔU=0:
0=Q+W⟹Q=−W
- The work done during an isothermal expansion of an ideal gas can be calculated using the formula:
W=−nRTln(V2V1)
- Here, n is the number of moles, R is the universal gas constant, T is the absolute temperature, V2 is the final volume, and V1 is the initial volume.
- Now substituting the expression for W into the equation for Q:
Q=−(−nRTln(V2V1))=nRTln(V2V1)
- Thus, we can express Q as:
Q=nRTln(V2V1)
- Finally, check the provided options to find the one that matches this derived expression for Q.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - NCERT EXEMPLAR PROBLEMS
11 Videos
- THE S-BLOCK ELEMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE S-BLOCK ELEMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
For an isothermal process
View SolutionIn an isothermal process
View SolutionFor an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using expression =−nRTln.VfVi. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversible to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option
View SolutionFor an isothermal expansion of an ideal gas
View SolutionFor the reversible process, the value of ΔS is given by the expression:
View SolutionFor the reversible process, the value of ΔS is given by the expression:
View SolutionFor an ideal gas undergoing isothermal reversible expansion
View SolutionCalculate q,w, and ΔU for the isothermal reversible expansion of one mole of an ideal gas from an initial pressure of 2.0 bar to a final pressure of 0.2 bar at a constant temperature of 273K.
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
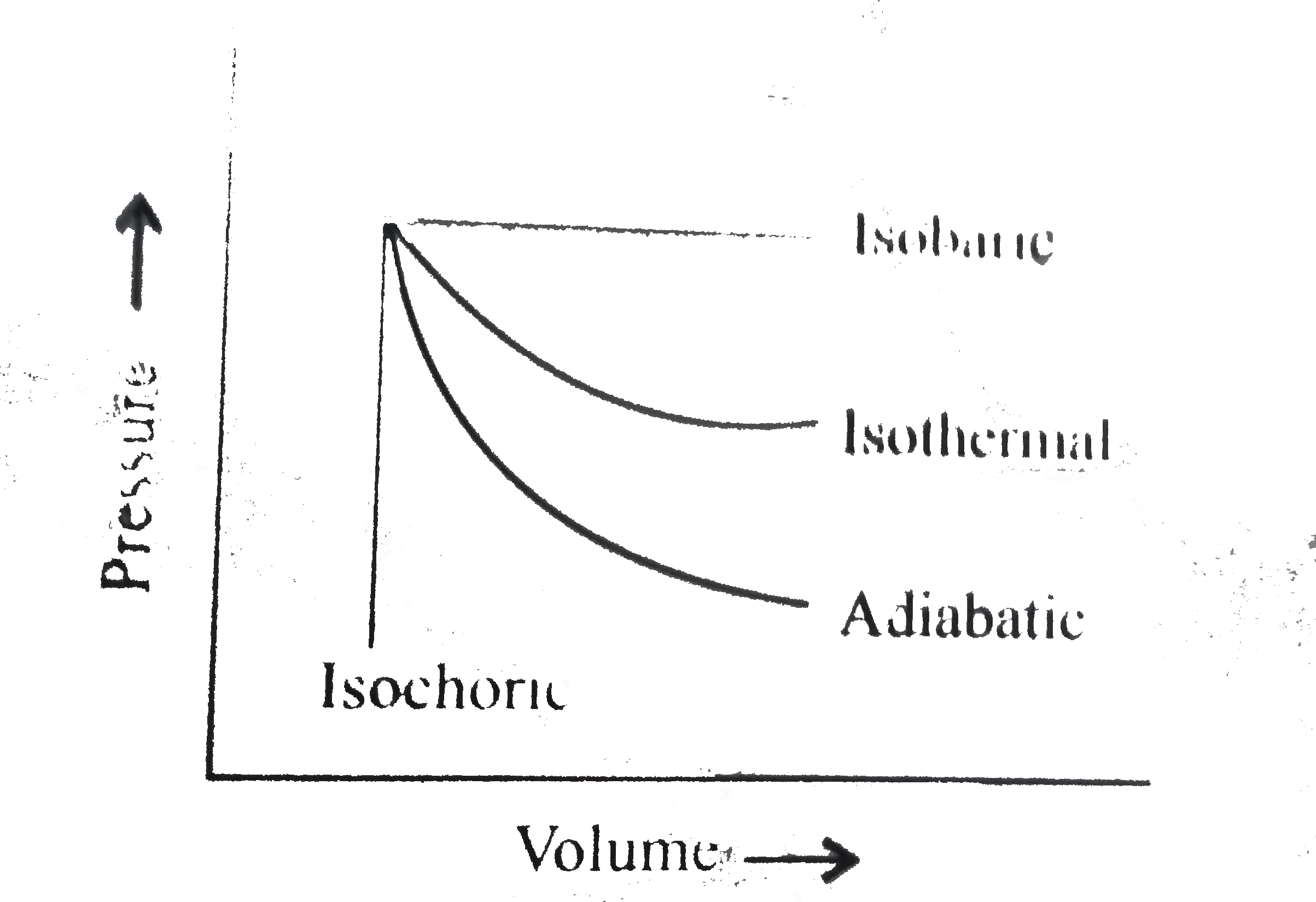
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
The q value and work done in isothermal reversible expansion of one mole of an ideal gas from initial pressure of 1 bar to final pressure of 0.1 bar at constant temperature 273K are:
View SolutionFor isothermal expansion , which is true?
View Solution
