For the ${[C o F_{6}]}_{6}^{3 -}$ ion the mean pairing energy is found to be $21000 c m^{- 1}$ . The magnitude of $Δ_{0}$ is $13000 c m^{- 1}$ . Calculate the crystal field stabilization energy for this complex ion corresponding to low spin and high spin states.

Text Solution

Verified by Experts

$C F S E (Δ E_{0}) = (E_{L F}) - (E_{i s o})$
$= {n t_{2 g} (- 0.4) + n_{e g} (0.6) Δ_{0} + n_{p}^{p}}$
$n t_{2 g}$ = no. of electrons in $t_{2 g}$ orbitals
$n_{e g}$ = no. of electron in $e_{g}$ orbitals
$n_{p}$ =no. of electron pairs in the ligand field
$n ._{p}$ =no. of electron pairs in the isotropic field (bary centre).
${[C o F_{6}]}_{6}^{- 3}$ , Co is in +6 oxidation state ( $d^{6}$ configuration)
For high spin complex: Electronic configuration in isotropic field

Electronic configuration (for high spin complex) $t_{2 g}^{4} e_{g}^{2}$

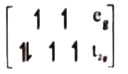
CFSE $(Δ E_{0}) (4 \times (- 0.4) + 2 \times 0.6] Δ_{0} + I P - 2$
$= [- 1.6 + 1.2] Δ_{0} + 1 P] - 2$
$= [- 0.4 Δ_{0} + 1 P] - 2$
$= - 2.4 Δ_{0} + 1 P$
given $Δ_{0} = 13000 c m^{- 1}, P = 21, 000 c m^{- 1}$
CFSE= $- 2.4 \times 13000 + 21, 000$
=-31200+21000
$= - 10200 c m^{- 1}$
For low spin complex : Electronic configuration in isotropic field

number of paired electron E is 0 (n.P)=2
Electronic configuration (for low spin complex ) $t_{2 g}^{6} e_{g}^{0}$

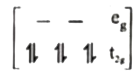
number of electron pairs in the ligand field =3
$C = (C F S E (Δ E_{0}) = [6 \times (- 0.4) + (0 \times 0.6)] Δ_{0} + 3 P] - 2$
$= [- 2.4 + 0] Δ_{0} + 3 P] - 2$
$= [- 2.4] Δ_{0} + 3 P] - 2$
$= - 0.4 Δ_{0} + 3 P$
given $Δ_{0} = 13000 c m^{- 1}, P = 21, 000 c m^{- 1}$
CFSE=-4 x 13000+ 3 x 21000
=-52000 + 63000
$= + 11, 000 c m^{- 1}$
The complex is less stable in the low spin state.

Updated on:21/07/2023

Crystal field stabilization energy for high spin $d^{4}$ octahedral complex is
A $- 1.8 Δ_{0}$
B $- 1.6 Δ_{0} + P$
C $- 1.2 Δ_{0}$
D $- 0.6 Δ_{0}$
Crystal field stabilization energy for high spin $d^{4}$ octahedral complex is
A $- 0.6 △_{\circ}$
B $- 1.8 △_{\circ}$
C-1.6 triangle_circ + p
D $- 1.2 △_{\circ}$
Crystal field stabilization energy for high spin $d^{4}$ octahedral complex is
A(a) $- 1.8 Δ_{0}$
B(b) $- 1.6 Δ_{0} + p$
C(c) $- 1.2 Δ_{0}$
D(d) $- 0.6 Δ_{0}$