For which of the following gas/gases, PCVCRTC close to 0.22?
Cl2
CH3OH
C2H4
CH4
The correct Answer is:B
Molecule having hydrogen bonding values of PCVCT close to 0.22
Topper's Solved these Questions
- STATES OF MATTERBOOK - A2ZCHAPTER - STATES OF MATTEREXERCISE - Liquid State
17 Videos
- STATES OF MATTERBOOK - A2ZCHAPTER - STATES OF MATTEREXERCISE - Section B - Assertion Reasoning
23 Videos
- STATES OF MATTERBOOK - A2ZCHAPTER - STATES OF MATTEREXERCISE - Kinectic Theory Of Gases, Maxwell Distribution Of Speed
45 Videos
- SOME BASIC PRINCIPALS OF ORGANIC CHEMISTRYBOOK - A2ZCHAPTER - SOME BASIC PRINCIPALS OF ORGANIC CHEMISTRYEXERCISE - Section D - Chapter End Test
60 Videos
Similar Questions
Knowledge Check
Which of the following gases boils at 0∘C
ACH4BCH3CH3CCH3CH2CH3DCH3CH2CH2CH3For which of the following gaseous reactions, the relationship log KCKP+log RT = 0 will bne correct ?
APCI5⇔PCI3+CI2BSO2+O2⇔2SO3C2NH3⇔N2+3H2DN2+O2⇔2NOWhich of the following gases has the least value of critical temperature (Tc) and critical pressure (pc) ?
AHeBH2CN2DCO2
Find the critical constant (Pc,Vc and Tc) in terms of A and B, also find compressibility factor ( z) for the following equation of state.
PV=RT−AV+2BV2
where && and B are constant, P =pressure and V=molar volume.
View SolutionTo an evacuated vessel with movable piston under external pressure of 1 atm 0.1 mole of He and 1.0 mole of an unknown compound vapour pressure 0.68 atm at 0∘C are introduced Considering the ideal gas behaviour the total volume (in litre) of the gases at 0∘C is close to .
View Solution
When pressure is increases at constant temp volume of gas decreases AB→gases,BC→vpour+liquCD→liqu
critical point: At this point all the physical propeties of liquid phase will be same as the physical properties in vapour such as, density of liquid = density of vapour
Tc or critical temp: Temperature abive which a gas can not be liquified
Pc or critical pressure: minimum pressure which must be applied at critical temp to convert the gas into liqid.
Vc or critical volume: volume occupied by one mole of gas at Tc&Pc
CRITICAL CONSTANT USING VANDERWAAL EQUATIONS:
(P+aV2m)(Vm−gb)=RT==⇒(PV2m+a)(Vm−b)=RTV2mPV3m+aVm−PbV2m−ab−RTV2m=0==⇒V3m+V2m(b+RTP)+aPVm−abP=0
since equation is cubic in Vm hence there will be three roots of equation of any temperature and pressure. At critical point all three roots will coincide and will given single value of Vm=Vc at critical point. Vander Waal equation will be
V3m−V2m(b+RTCPC)+aPCVm−abPC=0...(i)
But at critical point all three roots of the equation should be equal, hence equation should be:
Vm=Vc
(Vm−Vc)3=0
V3m−3V2mVc+3VmV2c−V3c=0..(2)
comparing with equation (1)
b+RTcPc=3Vc ...(i) aPc=3V2c ...(ii) abPc=V3c ..(iii)
From (ii) and (iii), Vc=3b
From (ii) Pc=a3V2c substituting Pc=a3(3b)2=a27b2
From (i) RTcPc=3Vc−b=9b−b=8b⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slope will be negative zero is the maximum value of slope.
(∂P∂Vm)TC=0..(i)∂∂Vm(∂P∂Vm)TC=0...(ii)
{Mathematically such points an known as point of inflection (where first two derivatives becimes zero)}
using the two TcPc and Vc can be calculated by

A scientist proposed the following equation of state P=RTVm−BV2m+CV3m. If this equation leads to teh critical behaviour then critical temperature is:
View SolutionKp and Kc are inter related as
Kp=Kc(RT)Δn
Answer the following questions:
In which of the following equilibria Kp is less than Kc?
View SolutionWhen perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
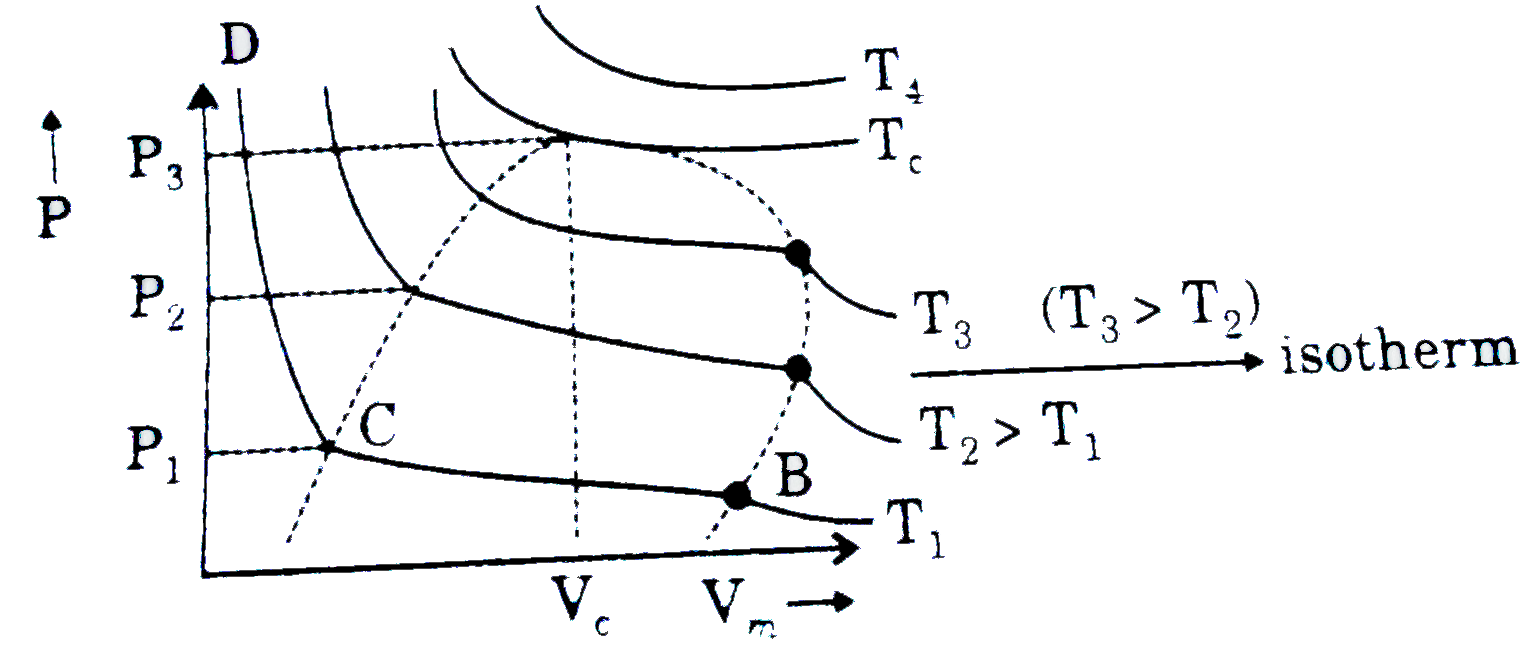
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
A scientist proposed the following equation of state
P=RTVm−BV2m+CV2m If this equation leads to the critical behaviour then critical temperature is
View Solution
