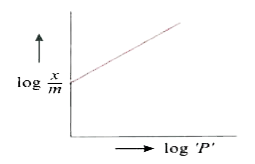
Freundlich adsorption isotherm is given by the expression $\frac{x}{m} = k p^{1 / n}$ . Which of the following conclusions can be drawn from this expression ?

A

When $\frac{1}{n} = 0,$ the adsorption is independent of pressure

B

When $\frac{1}{n} = 0,$ the adsorption is directly proporational to pressure

C

When $n = 0, \frac{x}{m}$ vs p graph is a line parallel to x-axis

D

When $n = 0,$ plot of $\frac{x}{m}$ vs p is a curve

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

$\frac{x}{m} = k p^{\frac{1}{n}} .$ When $\frac{1}{n} = 0, \frac{x}{m} = k p^{0} = k$ (constant) i.e., it becomes independent of pressure. Hence, (a) is correct and (b) is wrong. When $n = 0, \frac{x}{m} = k p^{\infty} .$ Hence, $\frac{x}{m} v s p$ cannot be linear parallel to x-axis but will be a curve. Hence, (c ) is wrong and (d) is correct.

|

Updated on:21/07/2023

Class 12 CHEMISTRY SURFACE CHEMISTRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Freundlich adsorption isotherm is given by the expression $\frac{x}{m} = k p^{1 / n}$ . Which of the following conclusions can be drawn from this expression ?
AWhen $\frac{1}{n} = 0,$ the adsorption is independent of pressure
BWhen $\frac{1}{n} = 0,$ the adsorption is directly proporational to pressure
CWhen $n = 0, \frac{x}{m}$ vs p graph is a line parallel to x-axis
DWhen $n = 0,$ plot of $\frac{x}{m}$ vs p is a curve
Question 2 - Select One
Freundlich adsorption isotherm is given by the expression $\frac{x}{m} = k P^{\frac{1}{n}}$ which of the following conclusions can be draw from this expression?
AWhen $\frac{1}{n} = 0$ , the adsorption is directly proportional to pressure
BWhen $n = 1, \frac{x}{m}$ vs $p$ graph is a line parallel to $x$ -axis
CWhen $\frac{1}{n} = 0$ the adsorption is independent of pressure
DWhen $n = 2$ , plot off $\frac{x}{m}$ vs $p$ is a rectangular hyperbola
Question 3 - Select One
Freundlich adsorption isotherm is given by the expression $\frac{x}{m} = k P^{\frac{1}{n}}$ which of the following conclusions can be draw from this expression?
AWhen $\frac{1}{n} = 0$ , the adsorption is directly proportional to pressure
BWhen $n = 1, \frac{x}{m}$ vs $p$ graph is a line parallel to $x$ -axis
CWhen $\frac{1}{n} = 0$ the adsorption is independent of pressure
DWhen $n = 2$ , plot off $\frac{x}{m}$ vs $p$ is a rectangular hyperbola

PRADEEP-SURFACE CHEMISTRY -MULTIPLE CHOICE QUESTIONS-II

Home
Ask Doubt
Profile