Geometrical isomerism is posible in :
CH3CH(CH3)CH2CH2CH3
CH3CH=CHCH3
CH3CH=CH2
ClH2C−CH2Cl
The correct Answer is:b
To determine which compound exhibits geometrical isomerism, we need to analyze the options provided based on the criteria for geometrical isomerism, which primarily occurs in alkenes with a carbon-carbon double bond (C=C). Here’s a step-by-step solution:
Step 1: Understanding Geometrical Isomerism
Geometrical isomerism occurs when there is restricted rotation around a double bond, leading to different spatial arrangements of groups attached to the carbon atoms. The two main forms are:
- Cis: Similar groups are on the same side of the double bond.
- Trans: Similar groups are on opposite sides of the double bond.
Step 2: Identify the Presence of a Double Bond
Geometrical isomerism is only possible in compounds that contain a carbon-carbon double bond. Therefore, we will look for alkenes (C=C) in the options provided.
Step 3: Analyze Each Option
1. Option 1: No double bond present.
- Since there is no double bond, geometrical isomerism is not possible.
2. Option 2: Contains a double bond (C=C) with different groups attached.
- Example: C=C with H and CH3 on one side and H and CH3 on the other side.
- Here, A (CH3) is not equal to B (H), allowing for both cis and trans configurations. Therefore, geometrical isomerism is possible.
3. Option 3: Contains a double bond but has two identical groups.
- Example: C=C with H and H on one side and CH3 and CH3 on the other side.
- Here, A (H) is equal to B (H), which means geometrical isomerism is not possible.
4. Option 4: Contains only single bonds.
- Since there is no double bond, geometrical isomerism is not possible.
Conclusion
After analyzing all options, Option 2 is the only compound that can exhibit geometrical isomerism due to the presence of a double bond and different substituents.
Final Answer
Geometrical isomerism is possible in Option 2.
---
Geometrical isomerism occurs when there is restricted rotation around a double bond, leading to different spatial arrangements of groups attached to the carbon atoms. The two main forms are:
- Cis: Similar groups are on the same side of the double bond.
- Trans: Similar groups are on opposite sides of the double bond.
Geometrical isomerism is only possible in compounds that contain a carbon-carbon double bond. Therefore, we will look for alkenes (C=C) in the options provided.
1. Option 1: No double bond present.
- Since there is no double bond, geometrical isomerism is not possible.
- Example: C=C with H and CH3 on one side and H and CH3 on the other side.
- Here, A (CH3) is not equal to B (H), allowing for both cis and trans configurations. Therefore, geometrical isomerism is possible.
- Example: C=C with H and H on one side and CH3 and CH3 on the other side.
- Here, A (H) is equal to B (H), which means geometrical isomerism is not possible.
- Since there is no double bond, geometrical isomerism is not possible.
After analyzing all options, Option 2 is the only compound that can exhibit geometrical isomerism due to the presence of a double bond and different substituents.
Geometrical isomerism is possible in Option 2.
Topper's Solved these Questions
- ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUES BOOK - DISHA PUBLICATIONCHAPTER - ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUES EXERCISE - Exercise - 1 : Concept Builder (Topicwise) TOPIC 3 : Concepts of Reaction Mechanism in Organic Compounds and Purification
31 Videos
- JEE MAIN 2019BOOK - DISHA PUBLICATIONCHAPTER - JEE MAIN 2019EXERCISE - MCQs
30 Videos
- POLYMERS BOOK - DISHA PUBLICATIONCHAPTER - POLYMERS EXERCISE - EXERCISE -2 : CONCEPT APPLICATOR
30 Videos
Similar Questions
Knowledge Check
Geometrical isomerism is possible in :
Aformaldehyde hydrozoneBacetone oximeCacetophebnone oximeDbenzophenone oximeGeometrical isomerism is possible in :
A B
B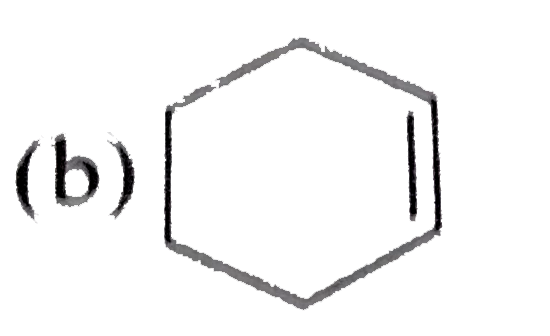 C
C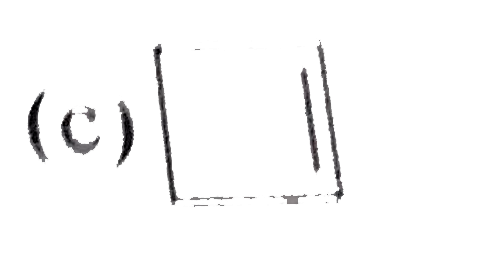 D
D
Geometrical isomerism is possible in
AAcetone-oxineBIsobuteneCAcetophenone-oximeDBenzophenone-oxime
