Given that ΔTf is the depression in freezing point of the solvent in a solution of a non-volatile solute of molarity m,the quantity Ltm→0(ΔTf/m) is equal to ……………. .
To solve the problem, we need to analyze the relationship between the depression in freezing point (ΔTf), molality (m), and molarity (M) of a solution containing a non-volatile solute.
1. Understanding the Depression in Freezing Point:
The depression in freezing point (ΔTf) is given by the formula:
ΔTf=i⋅Kf⋅m
where:
- i = van 't Hoff factor (which is 1 for non-volatile solutes),
- Kf = freezing point depression constant of the solvent,
- m = molality of the solution.
2. Relating Molality and Molarity:
For dilute solutions, molality (m) and molarity (M) can be approximately equal when the volume of the solvent is large. Thus, we can say:
m≈M(as M tends to 0)
3. Substituting Molality in the Freezing Point Depression Formula:
Since we are considering the limit as molarity (M) approaches 0, we can substitute molality (m) with molarity (M):
ΔTf=Kf⋅M
4. Finding the Limit:
We need to evaluate the limit:
limM→0ΔTfM
Substituting the expression for ΔTf:
limM→0Kf⋅MM
This simplifies to:
limM→0Kf=Kf
5. Conclusion:
Therefore, the quantity limM→0(ΔTfM) is equal to Kf.
Final Answer:
limM→0(ΔTfM)=Kf
The depression in freezing point (ΔTf) is given by the formula:
ΔTf=i⋅Kf⋅m
where:
- i = van 't Hoff factor (which is 1 for non-volatile solutes),
- Kf = freezing point depression constant of the solvent,
- m = molality of the solution.
For dilute solutions, molality (m) and molarity (M) can be approximately equal when the volume of the solvent is large. Thus, we can say:
m≈M(as M tends to 0)
Since we are considering the limit as molarity (M) approaches 0, we can substitute molality (m) with molarity (M):
ΔTf=Kf⋅M
We need to evaluate the limit:
limM→0ΔTfM
Substituting the expression for ΔTf:
limM→0Kf⋅MM
This simplifies to:
limM→0Kf=Kf
Therefore, the quantity limM→0(ΔTfM) is equal to Kf.
limM→0(ΔTfM)=Kf
Topper's Solved these Questions
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Exercises Archives (Subjective)
18 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.1 (Objective)
10 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Exercises Archives (Integer)
1 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Ex 1.2 (Objective)
9 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Archives Subjective
2 Videos
Similar Questions
Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
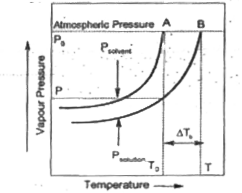
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal to
View SolutionWhy is boiling point of a solvent elevated upon the addition of a non-volatile solute ?
View Solution
Knowledge Check
The lowest freezing point of 0.1 M aqueous solution is of:
AK2SO4BNaClCUreaDGlucose
Why is freezing point depressed when a non-volatile solute is added to a solvent ?
View SolutionCalculate the ΔTf (depression in freezing point) of 0.4m solution of CH3COOH in benzene solution. Kf=xKkgmol−1.
View SolutionThe mole fraction of the solvent in the solution of a non-volatile solute is 0.980. The relative lowering of vapour pressure is :
View Solution0⋅1 M urea solution shows less depression in freezing point than 0⋅1MMgCl2 solution. Explain.
View SolutionThe freezing point of a 0.05 molal solution of a non-electrolyte in water is:
(Kf=1.86molality−1)
View SolutionIf ΔT is the elevation in boiling point of a solvent and m is the number of moles of the solute per kilogram of solute, what is the relationship between ΔT and m?
View SolutionIn coparison to a 0.01 M solution of glucose, the depression in freezing point of a 0.01 M MgCl2 solution is……
View Solution
