How many geometrical isomers are there fore
(a)[Co(NH3)2CI4]Θ
(b) [AuCI2Br2]Θ (square planar) (c ) [CuCI2Br2]2− (tetrahedral) .
Video Solution
Text Solution
Since [Co(NH3)2CI4]Θ is a[Ma2b4] type octahedral complex ion it has two geometrical isomers which are cis and trans as shown below
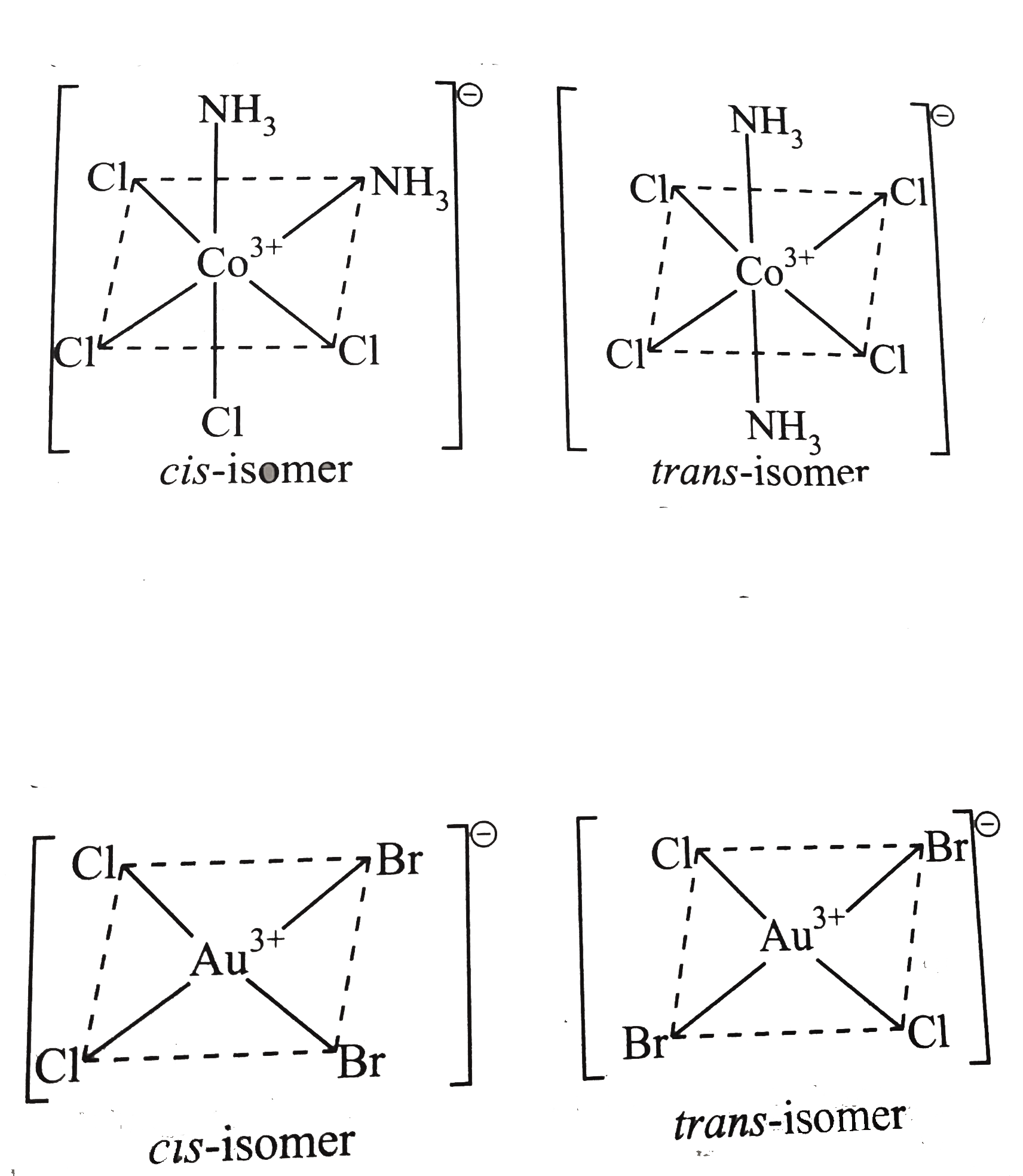
(b) Since [AuCI2Br2]Θ ion is [Ma2b2] type square planar complex ion it has two geometrical isomers viz cis and trans isomers
(c ) [CuCI2Br2]2− is tetrahedral and hence has no geometrical isomer .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Terminology)5videos
COORDINATION COMPOUNDS
- BOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Effective Atomic Number (Ean))3videos
COORDINATION COMPOUNDS
- BOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective18videos
COORDINATION COMPOUNDS
- BOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective23videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRYCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective29videos
D AND F BLOCK ELEMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of geometrical isomers for octahedral [Co(NH3)2Cl4]− and square planar [AuCl2Br2]− respectively are :
ATwo cis and trans, no geometrical isomersBTwo cis and trans, two cis and transCNo geometrical isomers, two cis and transDNo geometrical isomers, no geometrical isomer - Question 2 - Select One
The number of geometrical isomers for [Pt(NH3)2CI2] is
A3B4C1D2 - Question 3 - Select One
How many geometrical isomers are possible for [Pd2+(NH2−CH(CH3)−CO−2)2]0
A2B3C4D6
How many geometrical isomers are possible for the [Ni(NH3)4]2+?
View SolutionHow many geometrical isomers are possible for the complex ion [Cr(NH3)(OH)2CI3]2−.
View SolutionHow many isomers are possibel for the complex ion [Cr(NH3)(OH)2CI3]2− ?
View SolutionHow many geometrical isomers are possible for [Pd2+(NH2−CH(CH3)−CO−2)2]∘ ?
View SolutionThe number of geometrical isomers for octahedral [Co(NH3)2Cl4]− , square planar [AuCl2Br2]− respectviely are :-
View Solution
