How many orbital and how many electron are there in each of the first two principal quatum numbers ?
To determine how many orbitals and electrons are present in each of the first two principal quantum numbers (n=1 and n=2), we can follow these steps:
Step 1: Identify the Principal Quantum Numbers
The first two principal quantum numbers are:
- n = 1
- n = 2
Step 2: Determine the Subshells for n = 1
For n = 1:
- The possible values of the azimuthal quantum number (l) range from 0 to (n-1).
- Therefore, for n = 1: l can only be 0.
- l = 0 corresponds to the s subshell.
Step 3: Count the Orbitals for n = 1
- The s subshell has 1 orbital.
- Thus, for n = 1:
- Number of orbitals = 1
Step 4: Calculate the Number of Electrons for n = 1
- Each orbital can hold a maximum of 2 electrons (according to the Pauli Exclusion Principle).
- Therefore, for n = 1:
- Number of electrons = 1 orbital × 2 electrons/orbital = 2 electrons
Step 5: Determine the Subshells for n = 2
For n = 2:
- The possible values of l are 0 and 1 (since l can range from 0 to n-1).
- l = 0 corresponds to the s subshell, and l = 1 corresponds to the p subshell.
Step 6: Count the Orbitals for n = 2
- The s subshell (l = 0) has 1 orbital.
- The p subshell (l = 1) has 3 orbitals (px, py, pz).
- Therefore, for n = 2:
- Total number of orbitals = 1 (from s) + 3 (from p) = 4 orbitals
Step 7: Calculate the Number of Electrons for n = 2
- For the s subshell (1 orbital), the number of electrons = 1 orbital × 2 electrons/orbital = 2 electrons.
- For the p subshell (3 orbitals), the number of electrons = 3 orbitals × 2 electrons/orbital = 6 electrons.
- Therefore, for n = 2:
- Total number of electrons = 2 (from s) + 6 (from p) = 8 electrons
Summary of Results
- For n = 1:
- Number of orbitals = 1
- Number of electrons = 2
- For n = 2:
- Number of orbitals = 4
- Number of electrons = 8
The first two principal quantum numbers are:
- n = 1
- n = 2
For n = 1:
- The possible values of the azimuthal quantum number (l) range from 0 to (n-1).
- Therefore, for n = 1: l can only be 0.
- l = 0 corresponds to the s subshell.
- The s subshell has 1 orbital.
- Thus, for n = 1:
- Number of orbitals = 1
- Each orbital can hold a maximum of 2 electrons (according to the Pauli Exclusion Principle).
- Therefore, for n = 1:
- Number of electrons = 1 orbital × 2 electrons/orbital = 2 electrons
For n = 2:
- The possible values of l are 0 and 1 (since l can range from 0 to n-1).
- l = 0 corresponds to the s subshell, and l = 1 corresponds to the p subshell.
- The s subshell (l = 0) has 1 orbital.
- The p subshell (l = 1) has 3 orbitals (px, py, pz).
- Therefore, for n = 2:
- Total number of orbitals = 1 (from s) + 3 (from p) = 4 orbitals
- For the s subshell (1 orbital), the number of electrons = 1 orbital × 2 electrons/orbital = 2 electrons.
- For the p subshell (3 orbitals), the number of electrons = 3 orbitals × 2 electrons/orbital = 6 electrons.
- Therefore, for n = 2:
- Total number of electrons = 2 (from s) + 6 (from p) = 8 electrons
- For n = 1:
- Number of orbitals = 1
- Number of electrons = 2
- For n = 2:
- Number of orbitals = 4
- Number of electrons = 8
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Revision Exercises (Long Answer Questions)
6 Videos
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Revision Exercises (Numerical Problems)
6 Videos
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Revision Exercises (Very Short Answer Questions)
22 Videos
- STATES OF MATTER : GASES AND LIQUIDSBOOK - MODERN PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - UNIT PRACTICE TEST
13 Videos
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Unit Practice Test
12 Videos
Similar Questions
Knowledge Check
How many π electrons are there in
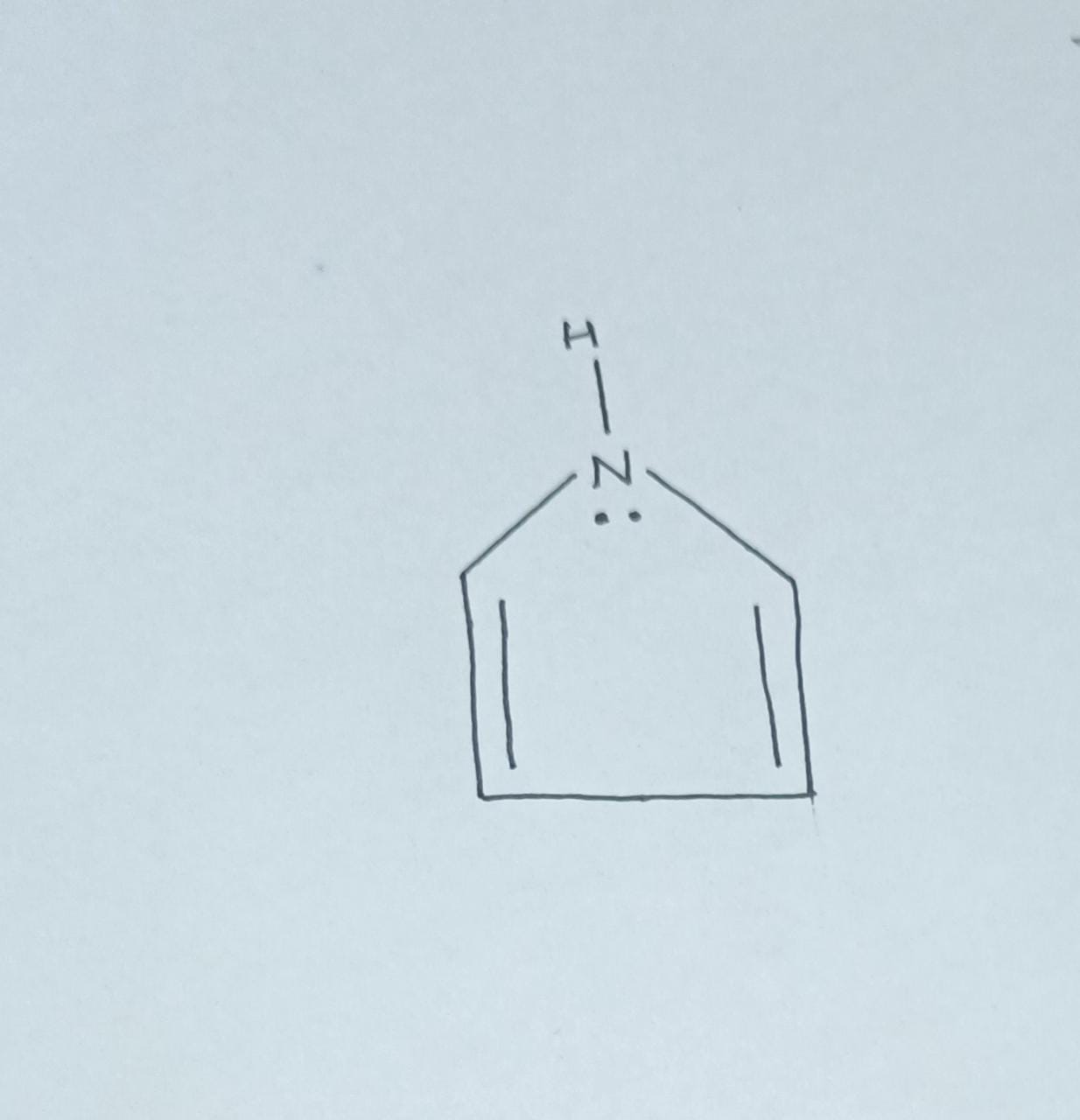 A2B4C6D8
A2B4C6D8How many electrons are there in Na+
A1B10C11D12How many electrons are there in Li2?
A4B6C5D3
How many electron states are there in a shell defined by the quantum number n=6?
View SolutionHow many electrons are there in the L-shell of chlorine atom?
View Solutionhow many orbits, orbitals and electrons are there in an atom having atomic mass 24 and atomic number 12?
View SolutionHow does the radius of orbit change with the principal quantum number?
View SolutionHow many electrons are there in one coulomb of electricity?
View Solution
