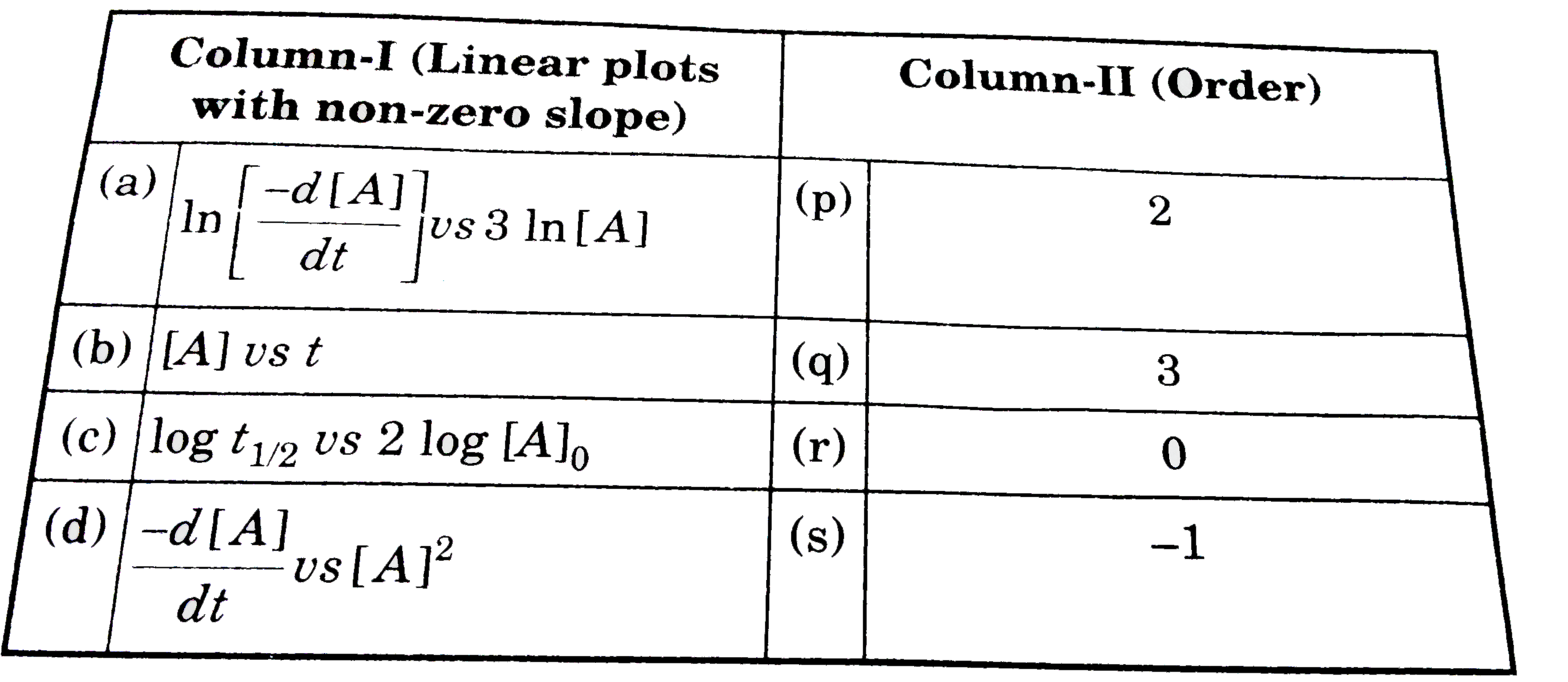If [A] is the concentration of A at any time t and [A]0 is the concentration at t=0 , then for the 1st order reaction , the rate equation can be written as _____.
k=2.303tlog[A][A0]
kt=2.303log[A0][A]
k=2.303tlog[A0][A0]−[A]
k=2.303tln[A0][A]
The correct Answer is:B
Rate expression .
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - MARVEL PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - TEST YOUR GRASP
50 Videos
- BIOMOLECULESBOOK - MARVEL PUBLICATIONCHAPTER - BIOMOLECULESEXERCISE - TEST YOUR GRASP
40 Videos
- CHEMICAL THERMODYNAMICS AND ENERGETICSBOOK - MARVEL PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND ENERGETICSEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP)
50 Videos
Similar Questions
Knowledge Check
If a is the initial concentration of the reaction and t1/2 is the half change time. Which of the following in true of the nth order reaction
At1/2∝an−1Bt1/2∝anCt1/2∝a1−nDt1/2∝an+1In a 1st order reaction, reactant concentration C varies with time t as:
A1/C increases linearly with tBlog C decreases linearly with tCC decreases with 1/tDlog C decreases with 1/tIn a 1st order reaction, reactant concentration C varies with time t as:
A1/C increases linearly with tBlog C decreases linearly with tCC decreases with 1/tDlog C decreases with 1/t
In a 1st order reaction, reactant concentration C varies with times t as:
View SolutionIf the rate of reaction A→B triples on increasing the concentration of A by 9 times, then the order of reaction is
View Solutiont1/4 can be taken as the time taken for concentration of reactant to drop to .3/4 of its initial value. If the rate constant for a first order reaction is K, then t1/4 can be written as:
View Solutiont1/4 can be taken as the time taken for concentration of reactant to drop to .3/4 of its initial value. If the rate constant for a first order reaction is K, then t1/4 can be written as:
View Solutiont14 can be taken as the time taken for the concentration of a reactant to drop to 34 of its initial value. If the rate constant for a first order reaction is k, the t14 can be writen as
View Solution