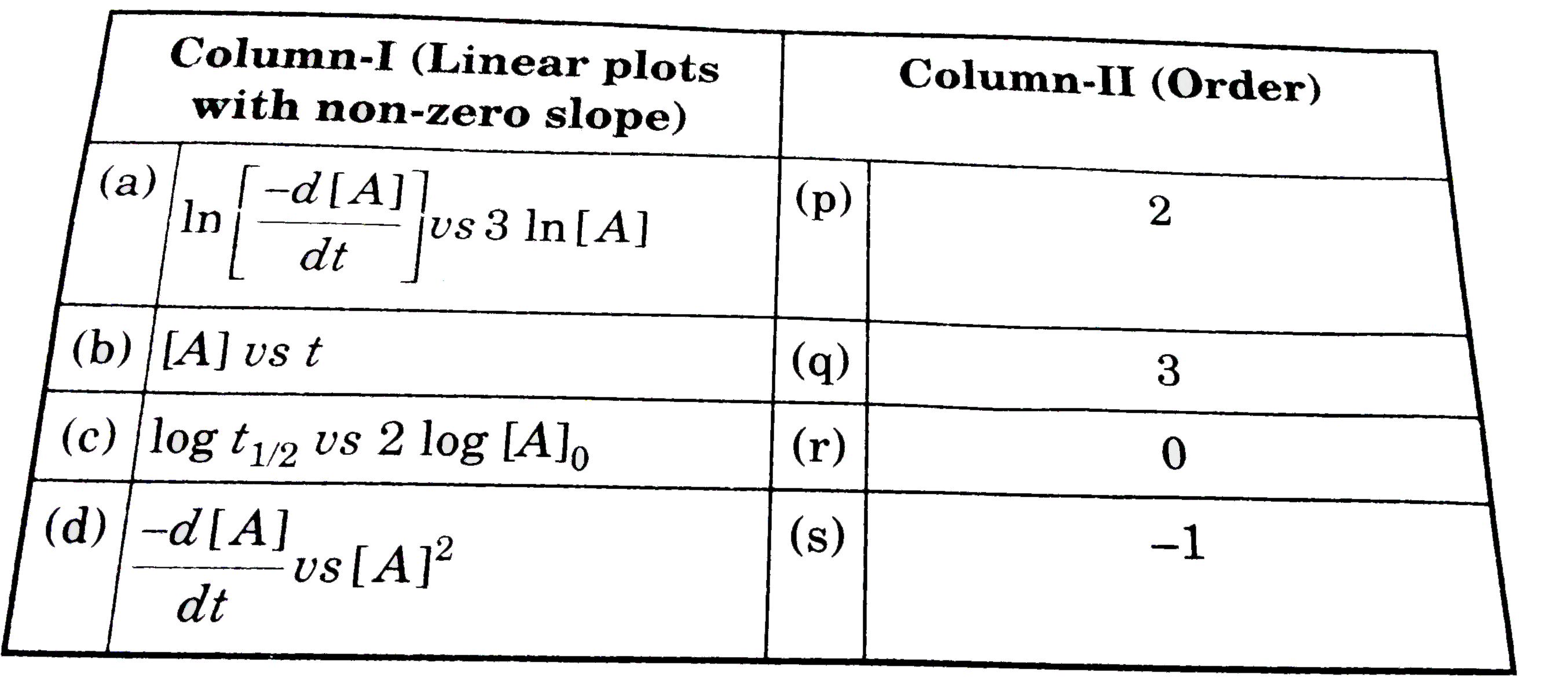If [A] is the concentration of A at any time t and [A]0 is the concentration at t=0 , then for the 1st order reaction , the rate equation can be written as _____.
k=2.303tlog10[A]t[A]0
kt=2.303log10[A]0[A]t
k=2.303tlog10[A]0[A]0−[A]t
k=2.303tlog10[A]0−[A]t[A]0
The correct Answer is:B
Step by step video, text & image solution for If [A] is the concentration of A at any time t and [A]_(0) is the concentration at t=0 , then for the 1^(st) order reaction , the rate equation can be written as _____. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - CRITICAL THINKING49videos
CHEMICAL KINETICS
- BOOK - TARGET PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - COMPETITIVE THINKING73videos
CHEMICAL KINETICS
- BOOK - TARGET PUBLICATIONCHAPTER - BIOMOLECULES EXERCISE - Evaluation Test10videos
BIOMOLECULES
- BOOK - TARGET PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND ENERGETICS EXERCISE - EVALUATION TEST25videos
CHEMICAL THERMODYNAMICS AND ENERGETICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If a is the initial concentration of the reaction and t1/2 is the half change time. Which of the following in true of the nth order reaction
At1/2∝an−1Bt1/2∝anCt1/2∝a1−nDt1/2∝an+1 - Question 2 - Select One
In a 1st order reaction, reactant concentration C varies with time t as:
A1/C increases linearly with tBlog C decreases linearly with tCC decreases with 1/tDlog C decreases with 1/t - Question 3 - Select One
In a 1st order reaction, reactant concentration C varies with time t as:
A1/C increases linearly with tBlog C decreases linearly with tCC decreases with 1/tDlog C decreases with 1/t
In a 1st order reaction, reactant concentration C varies with times t as:
View SolutionIf the rate of reaction A→B triples on increasing the concentration of A by 9 times, then the order of reaction is
View Solutiont1/4 can be taken as the time taken for concentration of reactant to drop to .3/4 of its initial value. If the rate constant for a first order reaction is K, then t1/4 can be written as:
View Solutiont1/4 can be taken as the time taken for concentration of reactant to drop to .3/4 of its initial value. If the rate constant for a first order reaction is K, then t1/4 can be written as:
View Solutiont14 can be taken as the time taken for the concentration of a reactant to drop to 34 of its initial value. If the rate constant for a first order reaction is k, the t14 can be writen as
View Solution