If PQRS are four different ligands, then how many geometric isomers will be found for square planar [Pt.PQRS]2+ ?
The correct Answer is:3
To determine the number of geometric isomers for the complex (Pt(PQRS))2+ where PQRS are four different ligands, we can follow these steps:
Step 1: Understand the Geometry
The complex is square planar, which means that the ligands will be arranged in a two-dimensional plane around the central platinum ion.
Step 2: Fix One Ligand
To simplify the counting of isomers, we can fix one ligand in a position. Let's fix ligand P at one position.
Step 3: Position the Remaining Ligands
With P fixed, we need to arrange the remaining three ligands (Q, R, and S) in the remaining three positions. The arrangement of these ligands will determine the geometric isomers.
Step 4: Identify Possible Arrangements
1. First Arrangement: Place Q opposite P. The remaining two ligands R and S can be arranged in the other two positions. This gives us one geometric isomer:
- P, Q, R, S (with Q opposite P)
2. Second Arrangement: Place R opposite P. The remaining two ligands Q and S can be arranged in the other two positions. This gives us a second geometric isomer:
- P, R, Q, S (with R opposite P)
3. Third Arrangement: Place S opposite P. The remaining two ligands Q and R can be arranged in the other two positions. This gives us a third geometric isomer:
- P, S, Q, R (with S opposite P)
Step 5: Count the Isomers
From the arrangements above, we can see that there are three distinct geometric isomers possible when P is fixed and the opposite ligand is varied among Q, R, and S.
Conclusion
Thus, the total number of geometric isomers for the complex (Pt(PQRS))2+ is 3.
The complex is square planar, which means that the ligands will be arranged in a two-dimensional plane around the central platinum ion.
To simplify the counting of isomers, we can fix one ligand in a position. Let's fix ligand P at one position.
With P fixed, we need to arrange the remaining three ligands (Q, R, and S) in the remaining three positions. The arrangement of these ligands will determine the geometric isomers.
1. First Arrangement: Place Q opposite P. The remaining two ligands R and S can be arranged in the other two positions. This gives us one geometric isomer:
- P, Q, R, S (with Q opposite P)
2. Second Arrangement: Place R opposite P. The remaining two ligands Q and S can be arranged in the other two positions. This gives us a second geometric isomer:
- P, R, Q, S (with R opposite P)
- P, S, Q, R (with S opposite P)
From the arrangements above, we can see that there are three distinct geometric isomers possible when P is fixed and the opposite ligand is varied among Q, R, and S.
Thus, the total number of geometric isomers for the complex (Pt(PQRS))2+ is 3.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 24- HALOALKANES AND HALOARENES15videos
CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 25- ALCOHOLS, PHENOLS AND ETHER15videos
CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22- THE D- AND F-BLOCK ELEMENTS15videos
CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - BIOMOLECULES EXERCISE - Exercise - 2 : Concept Applicator30videos
BIOMOLECULES
- BOOK - DISHA PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTURE EXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
CHEMICAL BONDING AND MOLECULAR STRUCTURE
Similar Questions
Knowledge Check
- Question 1 - Select One
How many geometrical isomers are possible for
 A2B3C4D8
A2B3C4D8 - Question 2 - Select One
How many geometrical isomers of this compound are possible ?
 A0B2C3D4
A0B2C3D4 - Question 3 - Select One
How many geometrical isomers of this compound are possible:
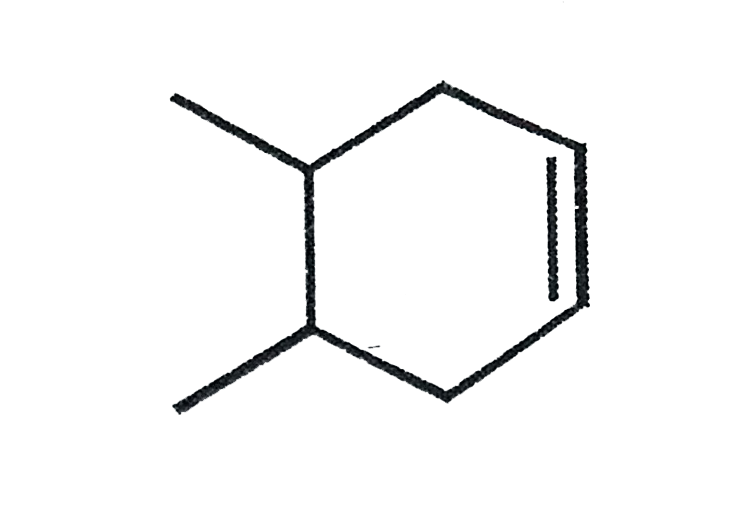 A0B2C3D4
A0B2C3D4
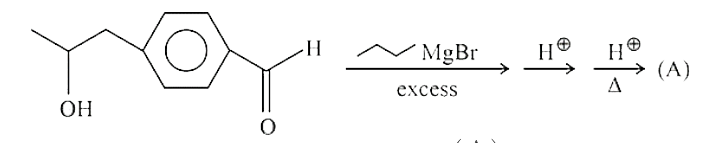
How many geometrical isomer of (A) is possible?View Solution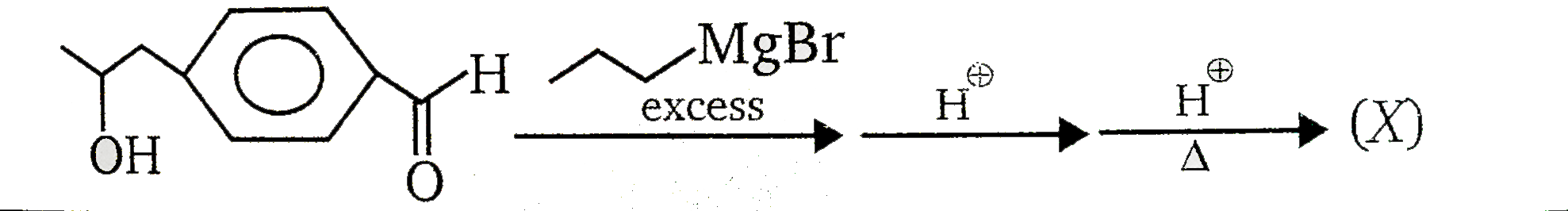
How many geometrical isomer of (X) is possible ?View Solution
How many geometrical isomers are possible for the above compound ?View Solution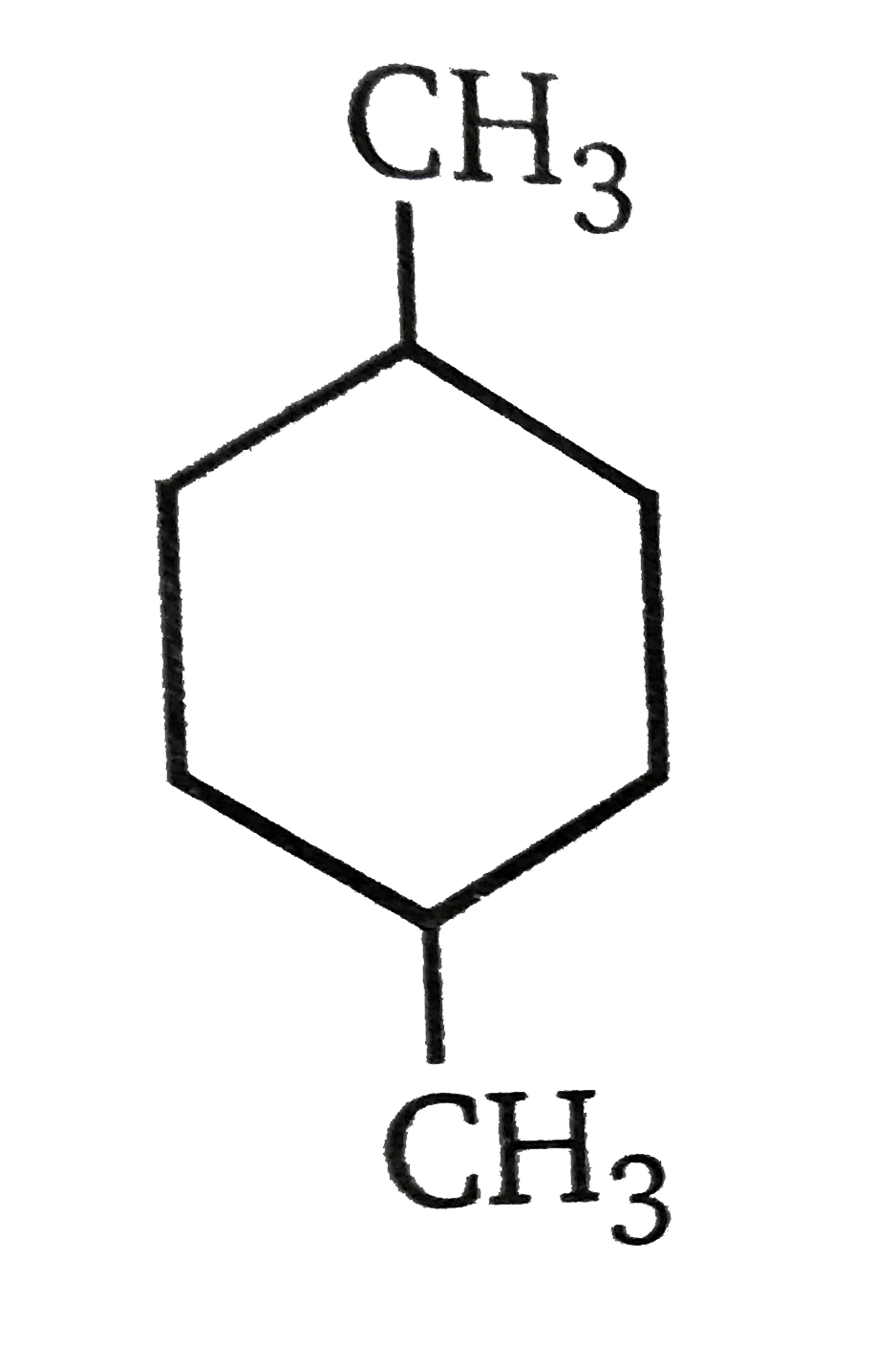
How many geometrical isomers are possible for the above compound ?View Solution
How many geometrical isomers are possible for the above compound ?View Solution



