In a crystalline solid, atoms of X form fcc packing and atoms of Y occupy all octahedral voids. If all the atoms along one body diagonal are removed, what is the simplest formula of the crystalline lattice solid?
The correct Answer is:
Number of atoms of X in fcc packing
Number of atoms of Y at octahedral voids = 4
Along one body diagonal, there are two X atoms and one Y atom.
Number of effective atoms of X after removal =
Number of effetive atoms of Y after removal = 4-1=3
Simplest formula of the solid .
Topper's Solved these Questions
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - MULTIPLE CHOCIE QUESTION (TYPE-I)63videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - ASSIGNMENT134videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - HIGHER ORDER THINKING SKILLS (HOTS) QUESTIONS7videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - REDOX REACTIONSEXERCISE - Ultimate Preparation9videos
REDOX REACTIONS
- BOOK - DINESH PUBLICATIONCHAPTER - SOLUTIONS EXERCISE - ULTIMATE PREPARATORY PACKAGE10videos
SOLUTIONS
Similar Questions
In a crystalline solid, atom of A form fcc packing and atoms of B occupy all octahedral voids. If all the atoms along one body diagonal are removed then what will be the simplest formula of the crystalline solid ?
View SolutionA crystal is made of particles X,Y and Z.X form fcc packing . Y occupies all the octahedral void of X and Z occupies all the tetrahedral voids of X . If all the particles along one body diagonal are removed then the formula of the crystal would be:
View Solution
Knowledge Check
- Question 1 - Select One
In a crystalline solid,atoms of X from fcc packing and the atoms of Y occupy all octahedral voids.If the atoms along one body diagnal are removed then the simplest formula of the crystalline solid will be:
AXYBX4Y3CX5Y4DX4Y5 - Question 2 - Select One
A crystal is made of particles X and Y.X form fcc packing and Y occupies all the octahedral voids . If all the particles along one body diagonal are removed then the formula of the crystal would de :
AX4Y3BX5Y5CX4Y5DNone of these - Question 3 - Select One
A crystal is made up of particles A. B and C. A forms fcc packing, B occupies all octahedral voids and C occupies all tetrahedral voids. If all the particles along one body diagonal are removed, then the formula of the crystal would be
AABC2BA2BC2CA8B4C5DA5B4C8
A crystal is made of particle X,Y and Z 'X' forms +FCC packing+. 'Y' occupies all the octahedral voids of X and Z occupies all tetrahedral voiods of X. If all the particles along one body diagonal are removed, then the formula of the crystal would be?
View SolutionA crystal is made up of particals X, Y, and Z. X froms f packing. Y occupies all octahedral voids of X and Z occupies all tetrahedral voids of X. If all the particles along one body diagonal are removed. Then the fromula of the crystal would be
View SolutionA crystalline solid is made of X, Y and Z elements. Atoms of X form fcc packing , atoms of Y occupy octahedral voids while atoms of Z occupy tetrahedral voids. What will be the simplest formula of solid if atoms along one body diagonal are removed ?
View SolutionA crystal is made of particles A and B. A forms FCC packing and B occupies all the octahedral voids. If all the particles along the plane as shown in figure are removed, then the formula of the crystal would be :
View SolutionA crystal is made of particles A and B . From fcc packing and B occupies all the octahedral voids . If all the particle along the plane as shown in figure are removed , then, the formula of the crystal would be :
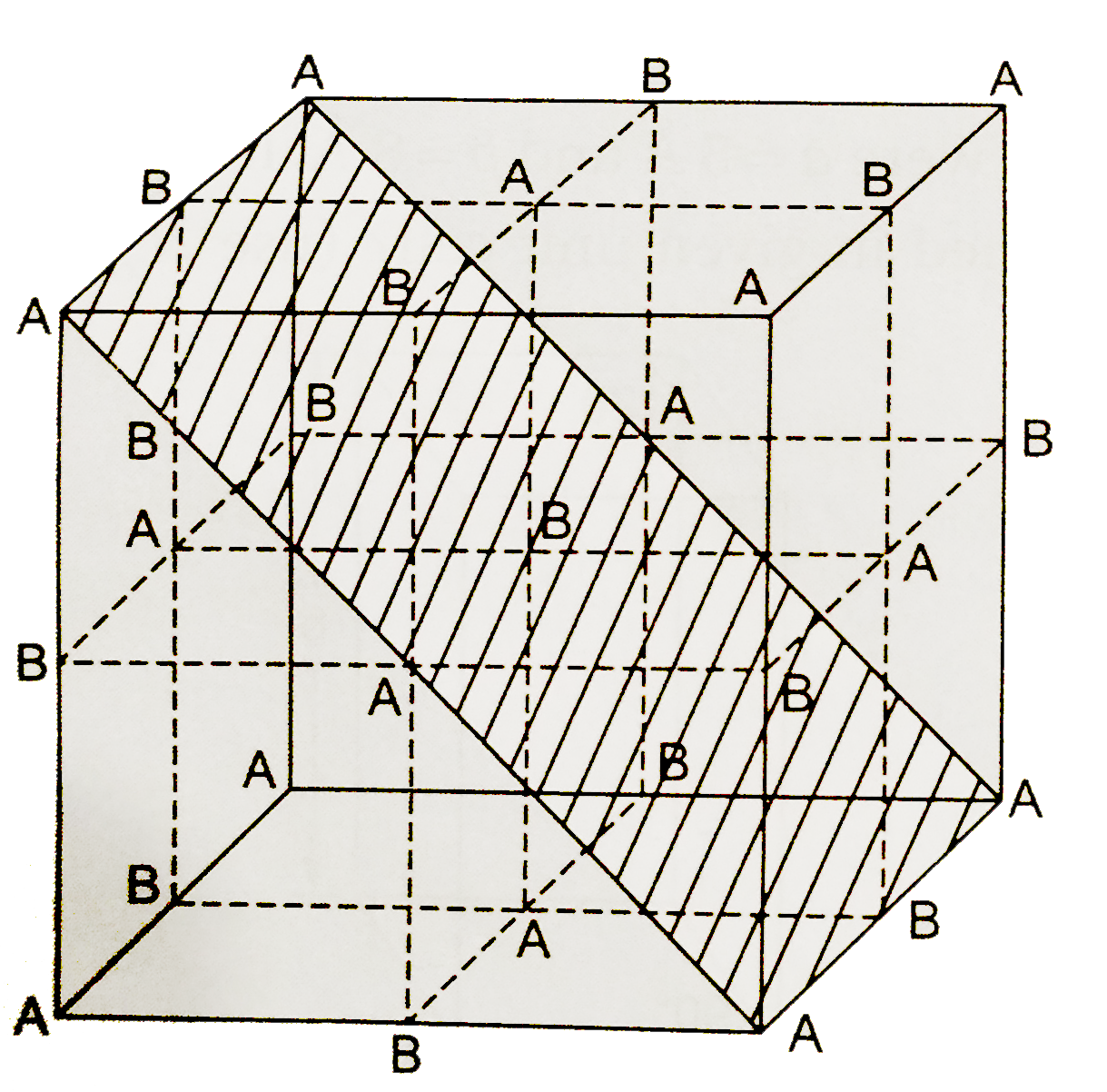 View Solution
View Solution

