In a measurement of quantum efficiency of photosynthesis in green plants, it was found that 10 quanta of red light of wavelength 6850 Å were needed to release one molecule of . The average energy storage in this process for 1 mol evolved is 112 Kcal.
What is the energy conversion efficieny in this experiment?
Given: 1 cal =4.18 J, J.s
23.5
26.9
66.34
73.1
The correct Answer is:B
To solve the problem of calculating the energy conversion efficiency in the experiment measuring the quantum efficiency of photosynthesis, we will follow these steps:
Step 1: Calculate the energy of one quantum of light
The energy E of a photon (quantum of light) can be calculated using the formula:
E=hcλ
where:
- h=6.63×10−34J.s (Planck's constant)
- c=3×108m/s (speed of light)
- λ=6850Å=6850×10−10m (wavelength in meters)
Substituting the values:
E=(6.63×10−34J.s)(3×108m/s)6850×10−10m
Calculating this gives:
E≈2.9×10−19J
Step 2: Calculate the total energy for 10 quanta
Since 10 quanta of light are needed to release one molecule of O2:
Total energy=10×E=10×2.9×10−19J=2.9×10−18J
Step 3: Convert the energy storage for 1 mole of O2
The average energy storage for 1 mole of O2 evolved is given as 112 Kcal. We need to convert this into Joules:
Energy in Joules=112Kcal×1000cal/Kcal×4.18J/cal=468256J
Step 4: Calculate the energy per molecule of O2
To find the energy storage per molecule, we divide the total energy by Avogadro's number NA=6×1023:
Energy per molecule=468256J6×1023≈7.8×10−19J
Step 5: Calculate the energy conversion efficiency
The energy conversion efficiency can be calculated using the formula:
Efficiency=(Energy stored per moleculeTotal energy for 10 quanta)×100
Substituting the values:
Efficiency=(7.8×10−19J2.9×10−18J)×100≈26.9%
Final Answer
The energy conversion efficiency in this experiment is approximately 26.9%.
---
The energy E of a photon (quantum of light) can be calculated using the formula:
E=hcλ
where:
- h=6.63×10−34J.s (Planck's constant)
- c=3×108m/s (speed of light)
- λ=6850Å=6850×10−10m (wavelength in meters)
E=(6.63×10−34J.s)(3×108m/s)6850×10−10m
Calculating this gives:
E≈2.9×10−19J
Since 10 quanta of light are needed to release one molecule of O2:
Total energy=10×E=10×2.9×10−19J=2.9×10−18J
The average energy storage for 1 mole of O2 evolved is given as 112 Kcal. We need to convert this into Joules:
Energy in Joules=112Kcal×1000cal/Kcal×4.18J/cal=468256J
To find the energy storage per molecule, we divide the total energy by Avogadro's number NA=6×1023:
Energy per molecule=468256J6×1023≈7.8×10−19J
The energy conversion efficiency can be calculated using the formula:
Efficiency=(Energy stored per moleculeTotal energy for 10 quanta)×100
Substituting the values:
Efficiency=(7.8×10−19J2.9×10−18J)×100≈26.9%
The energy conversion efficiency in this experiment is approximately 26.9%.
Topper's Solved these Questions
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 1)
3 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Level 3 (Passage 2)
4 Videos
- ATOMIC STUCTUREBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ATOMIC STUCTUREEXERCISE - Subjective problems
1 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
Similar Questions
Bond dissociation on energy of Cl2 is 240 kJ/mol. The longest wavelength of photon that can break this bond would be [NA=6×1023,h=6.6×10−34Js]
View SolutionWhat is the (a) momentum (b) speed and (c) de-Broglie wavelength of an electron with kinetic energy of 120 eV. Given h=6.6×10−34Js,me=9×10−31kg,1eV=1.6×10−19J.
View Solution
Knowledge Check
The de Broglie wavelength of an electron with kinetic energy 120 e V is (Given h=6.63×10−34Js,me=9×10−31kg,1eV=1.6×10−19J)
A2.13Ã…B1.13Ã…C4.15Ã…D3.14Ã…
If de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given h=6.6×10−34 Js ,
e=1.6×10−19 C, me=9.11×10−31 kg.
View SolutionGas molecules each of mass 10−26 kg are taken in a container of volume 1dm3 . The root mean square speed of gas molecules is 1 km sec−1 .What is the temperature fo gas molecules.
(Given : NA=6×1023,R=8J/mol.K)
View SolutionA microscope using suitable photons is employed to an electron in an atom within a distance of 0.1Å. What is the uncertainty involved in the measurment of its velocity? Mass of electron =9.11×10−31kg and h=6.626×10−34Js
View SolutionLight of wavelength 4000Å is incident on barium. Photoelectrons emitted describe a circle of radius 50 cm by a magnetic field of flux density 5.26×10−6tesla. What is the work function of barium in eV? Given h=6.6×10−34Js,e=1.6×10−19C,me=9.1×10−31kg.
View SolutionIf an electron has an energy such that its de Broglie wavelength is 5500Å, then the energy value of that electron is (h=6.6×10−34) Js, mc=9.1×10−31 kg
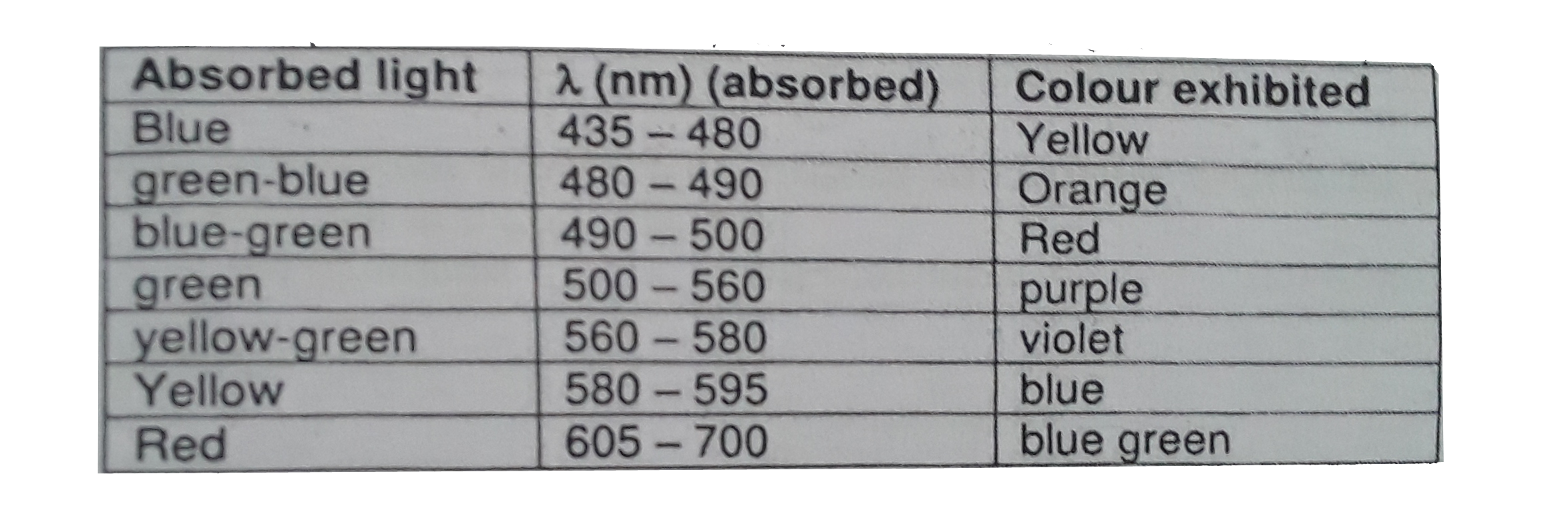
View SolutionThe value of Δ0 for [Ti(H2O)6]3+ is found to be 240 kJ mol−1 then predict the colour of the complex using the following table . (h=6×10−34J−sec,NA=6×1023c=3×108m/sec)
View SolutionThe wavelength of light in the visible region is about 390nm for violet color, about 550nm (average wavelength) for yellow green colour and about 760nm for red color. What are the energies of photon in eV at the (i) violet end (ii) average wavelength yellow-green color and (iii) red end of the visible spectrum? (Take h=6.63×10−34Jsand1eV=1.6×10−19Js)
View Solution
