In Schrodinger wave mechanical model Ψ2(r,θ,ϕ) represents :
amplitude of electron wave
probability density of electron
total probaility of finding electron around nucleus
orbit
Step by step video & image solution for In Schrodinger wave mechanical model Psi^(2)(r,theta,phi) represents : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
wave mechanical model of the atom depends upon:
View SolutionColumn–I and Column–II contain data on Schrondinger Wave–Mechanical model, where symbols have their usual meanings. Match the columns.
Column-I
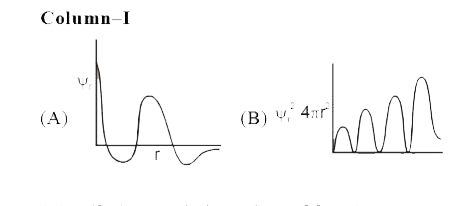
(C ) ψ(θ,ϕ)=K (independent of θ&ϕ)
(D) atleast one angular node is present
Column-II
(P)4s(Q)5px(R)3s(S)6dxy
View Solution
Knowledge Check
ψ2=0 represent
AnodeBorbitalCzero amplitude of waveDwave functionIn the Schrodinger's wave equation Ψ represents
AorbitBwave functionCwaveDradial probabilityΨ2=0 represents
Aa nodeBan orbitalCangular wave functionDwave function
On solving Schrodinger wave equation for hydrogen atom, the values of the enery obtained are called......and the corresponding values of the wavefunction (Ψ) are called.......
View SolutionOne of the major requirements of atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg uncertainity principal thorugh the concept of orbitals. The orbitals are defined as that 3d's space in which probability of finding electron maximum and are represented by wavefunctions ψn,l,m where n, l and m are quantum numbers. the variation of Ψ is analysed in terms of polar coordinates and hence ψ=f(r,θ,ϕ) where r' representes radius vector and θ and ϕ represents angle (∠) which the radius vector makes with z-axis and its projection in x-y plane makes with x-axis respectively. the expression ϕr,θ,ϕ are often given in terms of σ instead of r where σ=2zrna0 and z=atomic number of n=shell number
Which of the followings statements is incorrects with respect to ψ(r) vs r graph for H-atoms ?
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
Which of the following statement is incorrect with respect to Ψ(r)us. r graph for H-atom?
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
Which of the following wave function cannot represent an atomic orbital of H-atom?
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
If an orbital is represented as:
Ψr,0,ϕ=23(13α0)3/2.(σ−1)(σ2−8σ+12)
.σ−σ/2.cos0
belong to which orbital?
View Solution
