In terms of osmotic pressure (π) and volume of the solution (V) containing n moles of the solute, van't Hoff factor (i) at temperature T = …………….. .
To derive the expression for the van't Hoff factor (i) in terms of osmotic pressure (π), volume of the solution (V), number of moles of solute (n), and temperature (T), we can follow these steps:
Step 1: Understand the relationship of osmotic pressure
The osmotic pressure (π) of a solution can be expressed using the formula:
π=iCRT
where:
- π = osmotic pressure
- i = van't Hoff factor
- C = molarity of the solution (moles of solute per liter of solution)
- R = universal gas constant (0.0821 L·atm/(K·mol))
- T = temperature in Kelvin
Step 2: Express molarity (C) in terms of moles (n) and volume (V)
Molarity (C) can be defined as the number of moles of solute (n) divided by the volume of the solution (V) in liters:
C=nV
Step 3: Substitute molarity into the osmotic pressure equation
Now, substitute the expression for molarity (C) into the osmotic pressure equation:
π=i(nV)RT
Step 4: Rearranging the equation to solve for the van't Hoff factor (i)
To find the van't Hoff factor (i), we can rearrange the equation:
i=πVnRT
Final Expression
Thus, the expression for the van't Hoff factor (i) in terms of osmotic pressure (π), volume of the solution (V), number of moles of solute (n), and temperature (T) is:
i=πVnRT
The osmotic pressure (π) of a solution can be expressed using the formula:
π=iCRT
where:
- π = osmotic pressure
- i = van't Hoff factor
- C = molarity of the solution (moles of solute per liter of solution)
- R = universal gas constant (0.0821 L·atm/(K·mol))
- T = temperature in Kelvin
Molarity (C) can be defined as the number of moles of solute (n) divided by the volume of the solution (V) in liters:
C=nV
Now, substitute the expression for molarity (C) into the osmotic pressure equation:
π=i(nV)RT
To find the van't Hoff factor (i), we can rearrange the equation:
i=πVnRT
Thus, the expression for the van't Hoff factor (i) in terms of osmotic pressure (π), volume of the solution (V), number of moles of solute (n), and temperature (T) is:
i=πVnRT
Topper's Solved these Questions
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - CONCEPTUAL QUESTIONS
41 Videos
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - NCERT (QUESTIONS AND EXERCISES WITH ANSWERS)
13 Videos
- SOLUTIONSBOOK - PRADEEPCHAPTER - SOLUTIONSEXERCISE - TEST YOUR GRIP (MULTIPLE CHOICE QUESTIONS)
25 Videos
- REDOX REACTIONS BOOK - PRADEEPCHAPTER - REDOX REACTIONS EXERCISE - Assertion reason type question
16 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - PRADEEPCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Competition (FOCUS) JEE (Main and Advanced)/Medical Entrance SPECIAL (VIII. Assertion-Reason Type Questions)(Type II)
13 Videos
Similar Questions
Knowledge Check
If van't Hoff factor i=1,then
Ait is dissociationBIt is associationCBoth 1 and 2DNeither dissociation nor associationVan't Hoff factor is _____.
Aless than one in case of dissociationBalways more than oneCalways less than oneDless than one in case of associationFor a non-electrolytic solution, van't Hoff factor is equal to
A0B1C2Dbetween 0 -1
If a solute undergoes trimerization in solution, the minimum value of the van't Hoff factor is
View Solution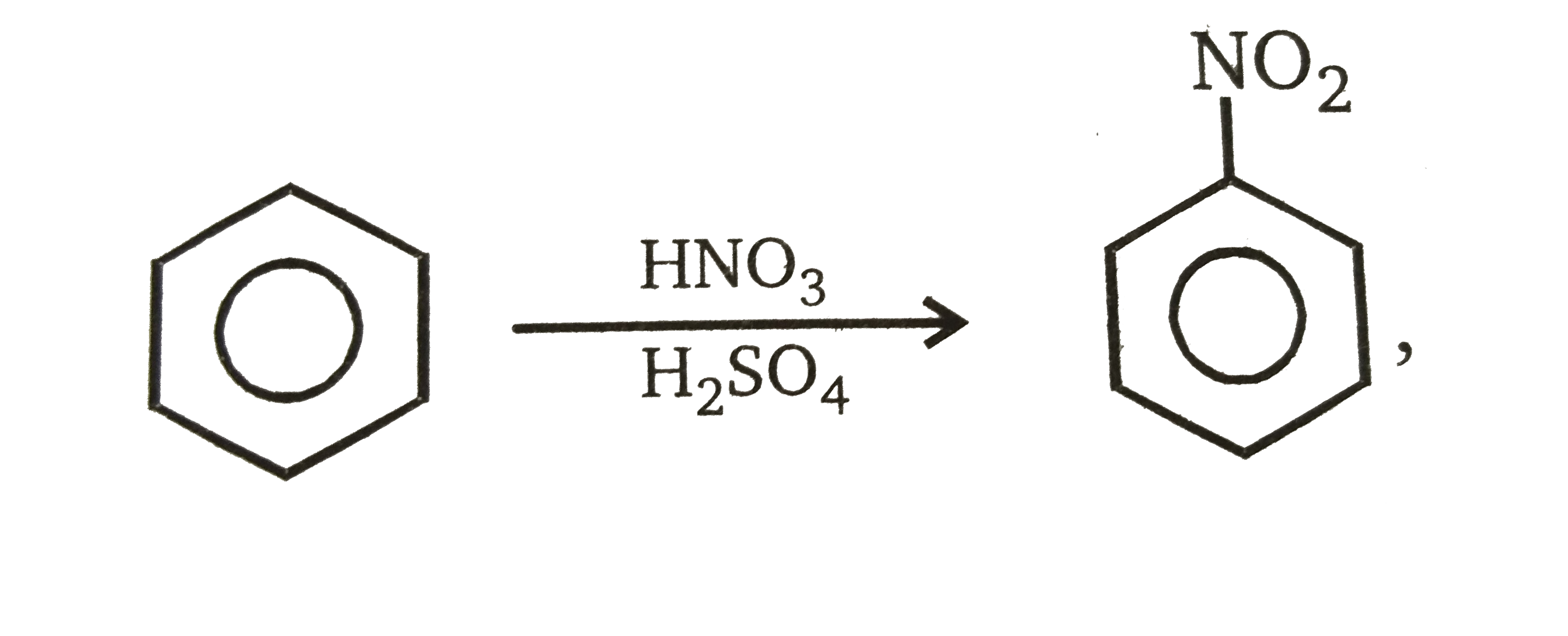 , van't -Hoff factor (i) for this reaction is:
, van't -Hoff factor (i) for this reaction is:
View SolutionFor a solution of a non-electrolyte in water, the van't Hoff factor is
View SolutionFor a solute undergoing association in a solvent, the van't hoff factor
View SolutionIn case a solute associates in solution, the van't Hoff factor,
View Solution