Indium -112 is radioactive and has a very short half-life (t1/2=14 min). Its decay constant and average life are repectively:
a) 0.0495 min−1, 9.7 min
b) 0.495min−1, 20.2 min
c) 9.7min−1,20.2 min
d) 0.0495min−1,20.2 min
Solution in Punjabi
0.0495 min−1, 9.7 min
0.495min−1, 20.2 min
9.7min−1,20.2 min
0.0495min−1,20.2 min
The correct Answer is:D
Step by step video & image solution for Indium -112 is radioactive and has a very short half-life (t_(1//2)=14 min). Its decay constant and average life are repectively: a) 0.0495 "min"^(-1), 9.7 min b) 0.495 "min"^(-1), 20.2 min c) 9.7 "min"^(-1),20.2 min d) 0.0495 "min"^(-1),20.2 min by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)1videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -21videos
SURFACE CHEMISTRY
Similar Questions
The following data pertain to reaction between A and B
S.No[A][B]RatemolL−1molL−1molL−1sec−1I1×10−22×10−22×10−4II2×10−22×10−24×10−4III2×10−24×10−28×10−4
Which of the following interference(s) can be drawn from the above data
(a) Rate constatnt of the reaction 10−4
(b) Rate law of reaction is k[A][B]
(c ) Rate of reaction increases four times on doubling the concentration of both the reactant Select the correct answer codes:
a) a,b and C
b) a and b
c) b and c
d) c alone01:24View Solutioncolumn Icolumn IIP.Zero order reaction1.t1/2α1[A]0Q.First order reaction2.t100%=[A]0/kR.second order reactions3.Involves at least two reactantsS.Pseudo unimolecular reaction4.[A]=[A]0e−kt
02:26View Solutionfor the graph below, select correct order of temperture ?
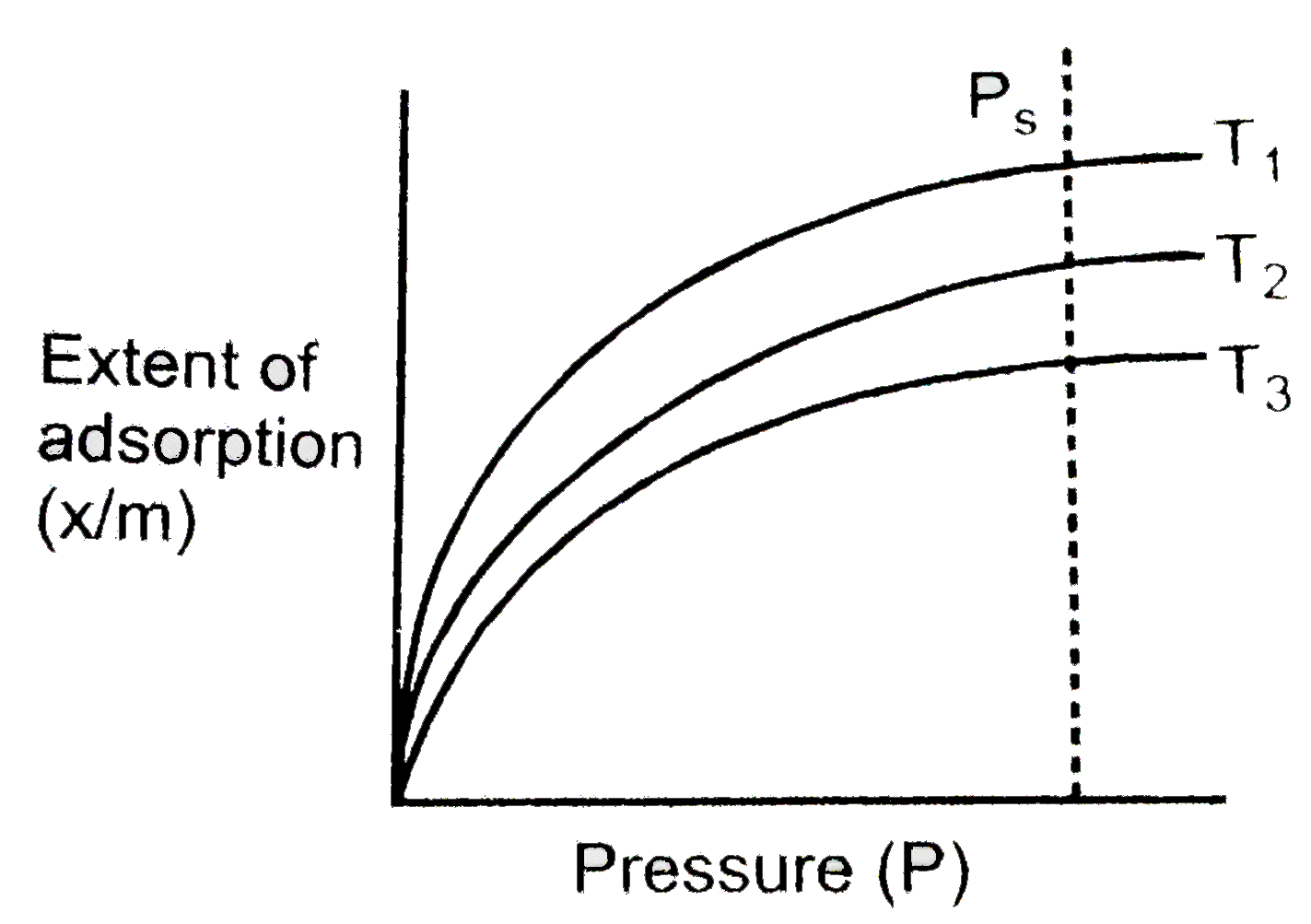 01:29View Solution
01:29View SolutionIf 49th of a bucket is filled in 1 minute, the rest of it will be filled in a. 1 min b. 94 min c. 54 min d. 45 min
02:27View SolutionHalf-life of radio active element A is 30 min while B is 20 min. Calculate ratio of number of nuclei decayed of A B after 60 min
00:36View SolutionA radioactive isotope decays at such a rate that after 96 min, only 1/8th of the original amount remains.
The value of t1/2 of this nuclide is
a. 12 min b. 32 min c. 24 min d. 48 min03:27View SolutionThe half-life period of a radioactive substance is 5 min . The amount of substance decayed in 20 min will be
03:07View SolutionIndium -112 is radioactive and has a very short half-life (t1/2=14 min). Its decay constant and average life are repectively:
03:01View SolutionThe average life of a radioactive element is 7.2 min. Calculate the time travel (in min) between the stages of 33.33% and 66.66% decay
04:12View SolutionIf the half-life period of a first order reaction is 138.6 min, then the value of decay constant for the reaction will be ("in min"^(-1))
08:00View SolutionThe half-life of a radioactive substance is 20 min. The approximate time interval (t2−t1) between the time t2 when 23rd of its has decayed and time t1 when 13rd of it had decayed is -
(A) 14 min
(B) 20 min
(C) 28 min
(D) 7 min01:40View SolutionThe rate constant and half-life of a first order reaction at temperature T1 are k1min−1andx1min , respectively and those at temperature T2 are k2min−1andx2 min , respectively. If T2>T1 , which is greater , x1 or, x2 ?
01:52View SolutionAt 380∘ the half-life period for thefirst order decomposition ofH2O2 is 360 min. The energy of activation of the reaction is 200 kJ mol−. Calculation the time required for 75% decomposition at450∘ C
(1) 20.35 min,
(2) 40.7 min
( c) 120 min
(d) 60 min06:10View SolutionIndium -112 is radioactive and has a very short half-life (t1/2=14 min). Its decay constant and average life are repectively:
01:46View SolutionThe average life of a radioactive element is 7.2 min. Calculate the time travel (in min) between the stages of 33.33% and 66.66% decay
02:10View SolutionHalf-life of radio active element A is 30 min while B is 20 min. Calculate ratio of number of nuclei decayed of A B after 60 min
03:02View Solution

