K is rate constant at temp T then value of log K is equal to :-
A
log A
The correct Answer is:D
Step by step video, text & image solution for K is rate constant at temp T then value of underset(Ttooo)lim log K is equal to :- by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - OBJECTIVE QUESTIONS (LEVEL-B) SET I
48 Videos
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - OBJECTIVE QUESTIONS (LEVEL-B) SET II
13 Videos
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE PROBLEMS
70 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - OP TANDONCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Integer
4 Videos
- Chemical Thermodynamics and ThermochemistryBOOK - OP TANDONCHAPTER - Chemical Thermodynamics and ThermochemistryEXERCISE - Self Assessment (Integer type).
3 Videos
Similar Questions
The rate of a reaction increases to 2.3 times when the temperature is raised form 300K to 310K. If Q is the rate constant at 300K, then the rate constant at 310K will be equal to
View SolutionThe rate of a certain reaction increases by 2.3 times when the temperature is raised form 300K to 310K. If k is the rate constant at 300K, then the rate constant at 310K will be equal to
View Solution
Knowledge Check
limx→0xlogsinx is equal to
AzeroB∞C1Dcannot be determinedGiven that k is the rate constant for some order of any reaction at temp. T then the value of limT→∞logk= (where A is the Arrhenius constant)
AA.2,303BAC2.303 ADlog AThe rate of a certain reaction increases by 2.5 times when the temperature is raised from 300K at 310K. If k is the rate constant at 300K then the rate constant at 310 K will be equal to
AkB2kC2.5kD3k
When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
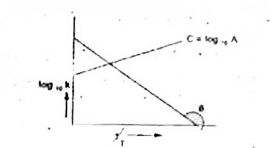
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate of certain reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If k is the rate constant at 300K then rate constant at 310K will be equal to
View SolutionIn Arrhenius equation K =Ae−Ea/RT, as limT→∞log10 K equals to:
View SolutionIf 5−k=1t, then the value of 53k is equal to :
View SolutionGraph between log k and 1/T [where K is rate constant in s−1 and T is the temperature (in K) is a straight line with Hence, Ea will be

View SolutionConsider the following statements.
i) Increase in concentration of rectant increases the rate of a zero order reaction.
ii) rate constant k is equal to collision frequency a if Ea=0
iii) rate constant k is equal to collision frequency A if Ea=∞.
iv) In k vs T is a straight line.
v) In k vs 1/T is a straight line.
Correct statements are:
View Solution
