Metal M of radius 50nm is crystallized in f type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of M at all faces of cubical crystal is 6×1030, then the area of one face of cubical crystal is A×1016m2. Find the value of A.
Video Solution
Text Solution
The correct Answer is:2
Consider one face of unit cell as show below.
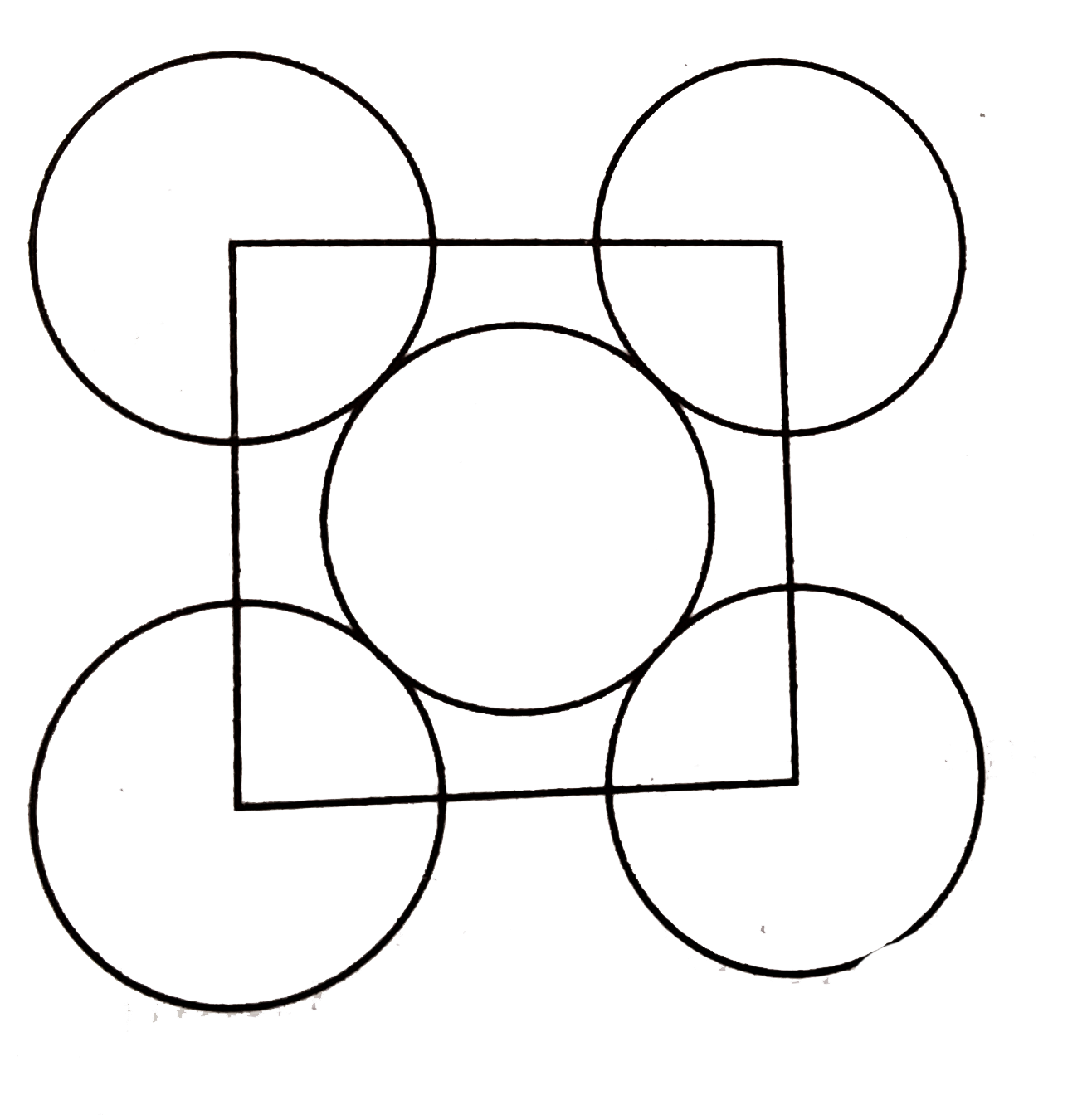
Number of atoms on one face
=4(corners) xx 1/8(percor≠rshare) + 1 (facecentre)
×12(face centre share)
=12+12=1/per face
Given number of atoms on all faces =6×1030
Given number of atoms on one face =16×1030
=1030 atoms
Number of unit cells at one face of crystal
=6×10306=1030
So, number of unit cells at the edge of crystal =√1030
=1015
Now, edge length of unit cell =4√2×50nm
Edge length of cubical crystal =4√2×50×1015nm
So, area of face of crystal =(4√2×50×1015)2nm2
=162×25×102×1030
=2×1034nm2
=2×10−18+34m2
=2×1016m2
∴A×1016m2=2×1016m2
A=2
|
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (Fill In The Blanks)
15 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (True/False)
19 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (Assertion-Reasoning)
19 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
3 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRYCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
Knowledge Check
What is the number of atoms in a unit cell of face-centred cubic crystal ?
A4B6C2D1The number of atoms in a unit cell of a cubic crystal system is 2, the arrangment of atoms is
Abody centred cubicBface centred cubicCend centred cubicDsimple cubicA metal with an atomic radius of 141.4 pm crystallizes in the face centered cubic structure. The volume of the unit cell in pm is -
A2.74×107B2.19×107C6.40×107D9.20×107
How many atoms constitute one unit cell of a face-centred cubic crystal?
View SolutionHow many atoms constitute one unit cell of a face-centered cubic crystal ?
View SolutionFor a cubic crystal, the face diagonal is 4.25Å. Calculate its face length.
View SolutionThe number of atoms in a unit cell of a cubic crystal system is 2, the arrangement of atoms is (A) body centred cubic
View SolutionLithium crystallizes in a body - centred cubic crystal .If the length of the unit cell if lithium is 315pm , the atomic radius of the lithium will be
View Solution
