Number of crystal systems having, only 2 types of Bravais lattices = x, Number of crystal systems having, at least 2 interfacial angles equal = y, All the three interfacial angles and all the three axes lengths equal = z Then find y−(x+z).
To solve the problem, we need to determine the values of x, y, and z based on the definitions provided in the question and then compute y−(x+z).
1. Identify x:
- We need to find the number of crystal systems that have only 2 types of Bravais lattices.
- The two types of Bravais lattices are:
- Tetragonal
- Monoclinic
- Therefore, x=2.
2. Identify y:
- We need to find the number of crystal systems that have at least 2 interfacial angles equal.
- The crystal systems that satisfy this condition are:
- Cubic (3 angles equal)
- Tetragonal (2 angles equal)
- Orthorhombic (3 angles equal)
- Monoclinic (2 angles equal)
- Triclinic (0 angles equal)
- Hexagonal (2 angles equal)
- Rhombohedral (3 angles equal)
- Counting these, we find that there are 6 crystal systems with at least 2 angles equal.
- Therefore, y=6.
3. Identify z:
- We need to find the number of crystal systems where all three interfacial angles and all three axes lengths are equal.
- The only crystal system that satisfies this condition is the cubic system.
- Therefore, z=1.
4. Calculate y−(x+z):
- Now we can substitute the values we found into the expression:
y−(x+z)=6−(2+1)=6−3=3
Final Answer:
y−(x+z)=3
- We need to find the number of crystal systems that have only 2 types of Bravais lattices.
- The two types of Bravais lattices are:
- Tetragonal
- Monoclinic
- Therefore, x=2.
- We need to find the number of crystal systems that have at least 2 interfacial angles equal.
- The crystal systems that satisfy this condition are:
- Cubic (3 angles equal)
- Tetragonal (2 angles equal)
- Orthorhombic (3 angles equal)
- Monoclinic (2 angles equal)
- Triclinic (0 angles equal)
- Hexagonal (2 angles equal)
- Rhombohedral (3 angles equal)
- Counting these, we find that there are 6 crystal systems with at least 2 angles equal.
- Therefore, y=6.
- We need to find the number of crystal systems where all three interfacial angles and all three axes lengths are equal.
- The only crystal system that satisfies this condition is the cubic system.
- Therefore, z=1.
- Now we can substitute the values we found into the expression:
y−(x+z)=6−(2+1)=6−3=3
y−(x+z)=3
Topper's Solved these Questions
Similar Questions
Number of crystal systems having only 2 types of bravais lattices = x, number of crystal system having at least two interfacial angles equal = y and number of crystal systems having all the three edge lengths equal = z. Then find the value of x×y×z.
View Solutionwhich of the following crystal structrues have length of all the crystallographic axis different and have at least one angle equal to 90∘?
View Solution
Knowledge Check
Which of the crystal systems has all the axial angles equal but not equal to 90∘?
ACubicBTetragonalCOrthorhombicDRhombohedralWhich type of crystal systems
(of the following ) have all their
interfacial angles right angle?ATriclinicBMonoclinicCOrthorhombicDHexagonalWhich of the crystal systems have all the axial distances (or edge lengths )equal?
ACube and rhombohedralBCubic and hexagonalCCubic and tetragonalDOnly cubic
the degree measure of three angles if a triangle are x,y and z If z=(x+y)/2 then find the value of z
View Solution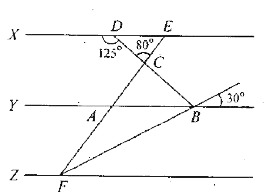
Three straight lines X, Y and Z are parallel and the angles are as shown in the figure above. What is ∠AFB equal to ?
View SolutionIf three real numbers x,y,z are in G.P. and x+y+z=ax then
View SolutionIf x,y,z are not all simultaneously equal to zero, satisfying the system of (sin3θ)x−y+z=0and(cos2θ)x+4y+3z=0, then the number of principal values of θ is
View SolutionA vector having magnitude 30 unit makes equal angles with each of X,Y, and Z -axes The components of vector along each of X,Y,and Z -axes are
View Solution
