Photon of wavelength 4×107 strikes on metal surface the work function of the metal being 2.13 eV Calculate (i) The energy of the photon ev (ii) The kinetic energy of the emission and (iii) the velocity of the photoelectron .
(1eV=1.6020×1019J)Solution in Gujrati
1eV=1.6020×1019∣∣ where λ=4×107m
=2.13eV×1.6020×1019J1eV
(i) Calculate of energy of photon
E=−hcλ=(6.626×1034Js)3.0×108ms−14×107m
(ii) Calculation of kinetic energy of emission
Kinetic energy of emission = (photon energy work function W )
=(4.9695×1019−3.4123×1019J
(iii) Calculation of velocity of the photoelectron kinetic energy 1.56×1019J
Kinetic energy =12mV2
v2=2×kinetic energy m
=√2×1.56×10199.1×1031kg
=√0.3429×1012kg−1
=0.5855×106ms−1
5.855×105ms−1
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - KUMAR PRAKASHANCHAPTER - STRUCTURE OF ATOMEXERCISE - Section -A (Try Your Self -1)
4 Videos
- STRUCTURE OF ATOMBOOK - KUMAR PRAKASHANCHAPTER - STRUCTURE OF ATOMEXERCISE - Section -A (Try Your Self -2)
5 Videos
- STATES OF MATTER BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - QUESTION PAPER FROM MODULE (SECTION - A)
4 Videos
- THE P-BLOCK ELEMENTSBOOK - KUMAR PRAKASHANCHAPTER - THE P-BLOCK ELEMENTSEXERCISE - SECTION-D NCERT EXEMPLAR SOLUTION (MCQs) LONG ANSWER
25 Videos
Similar Questions
Find neutron electron and proton in the following
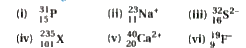
View SolutionCalculate the number of electron in one mole N−3 ion.
View SolutionGiven Dalton.s Law of partial Pressure, its mathematical formula and explain aqueous tension.
View SolutionDescribe the general trends in the following properties of the elements in Groups-13
Atomic size
View SolutionA photon of wavelength 5000λ strikes a metal surface with work function 2.20eV calculate
aTHe energy of the photon in eV
b. The kinetic energy of the emitted photo electron
c. The velocity of the photoelectron
View SolutionA photon of wavelength 4 xx 10^(-7) m strikes on metal surface , the work function fo the metal being 2. 13 eV Calculate : (i) the energy of the photon (ev) (ii) the kinetic energy fo the emission and the velocity fo the photoelectron ( 1 eV = 1 , 6020 xx 10^(-19) J) ,
View SolutionA photon of wavelength 4000Ã… A strikes a metal surface, then work function of the metal being 2.13 eV. Calculate (i) energy photoelectron and (iii) velocity of the photoelectron.
View SolutionA photon of wavelength 4xx 10^(-7) m strikes on metal surface, the work function of the metal being 2.13 eV. Calculate (i) the energy of the photon (eV) (ii) the kinetic energy of the emission and (iii) the velocity of the photoelectron (1 eV = 1.602 xx 10^(-19) J)
View Solutionयदि 4×10−7m तरंग-दैर्ध्य वाला एक फोटॉन 2.13eV कार्य -फलन वाली धातु की सतह से टकराता है तो (i) फोटॉन की ऊर्जा (eV ) में,(ii) उत्सर्जन की गतिज ऊर्जा, और (iii) प्रकाशीय इलेक्ट्रॉन के वेग का परिकलन कीजिए । (1eV=1.602×10−19J)
View Solutionएक धातु की सतह पर तरंग - दैर्घ्य 4×10−7 m वाले फोटॉन से प्रहार किया गया | धातु का कार्यफलन 2.13 eV है , तो (i ) फोटॉन की ऊर्जा eV में, (ii ) उत्सर्जित इलेक्ट्रॉन की गतिज ऊर्जा और (iii ) फोटोइलेक्ट्रॉन के वेग की गणना करे |
View SolutionA photon of wavelength 4×10−7m strikes on metal surface, the work function of the metal being 2.13 eV.
Calculate (1) the energy of the photon (eV).
(2) The kinetic energy of the emission.
View SolutionA photon of wavelength 4×10−7m strikes on metal surface , the work function of the metal being 2.13eV Calculate :
(i) the energy of the photon (ev)
(ii) the kinetic energy fo the emission and
the velocity of the photoelectron (1eV=1,6020×10−19J),
View SolutionA photon of wavelength 4x10−7 m strikes a metal surface work function of the metal is 2.13eV calculate
the kinetic energy of the emitted photoelectrons in eV
View SolutionA photon of wavelength 5000λ strikes a metal surface with work function 2.20eV calculate
aTHe energy of the photon in eV
b. The kinetic energy of the emitted photo electron
c. The velocity of the photoelectron
View SolutionA photon of wavelength '4 xx 10^(-7) m' strikes on metal surface, the work function of the. metal being '2.13 eV .' Calculate (i) the energy of the photon '(eV)',
View Solution
