Razia conducted an experiment in the field related to the rate of percolation. She observed that it took 40 min for 200 mL of water to percolate through the soil sample. Calculate the rate of percolation.
To calculate the rate of percolation, we can follow these steps:
Step 1: Identify the amount of water percolated
Razia observed that 200 mL of water was percolated through the soil sample.
Hint: Look for the total volume of water used in the experiment.
Step 2: Identify the time taken for percolation
The time taken for the 200 mL of water to percolate through the soil sample was 40 minutes.
Hint: Note the duration of the experiment to understand how long the water took to pass through the soil.
Step 3: Calculate the rate of percolation
The rate of percolation can be calculated using the formula:
Rate of Percolation=Amount of water percolatedTime taken
Substituting the values we have:
Rate of Percolation=200 mL40 min
Step 4: Perform the calculation
Now, we divide 200 mL by 40 minutes:
Rate of Percolation=5 mL/min
Conclusion
The rate of percolation is 5 mL per minute.
---
Razia observed that 200 mL of water was percolated through the soil sample.
The time taken for the 200 mL of water to percolate through the soil sample was 40 minutes.
The rate of percolation can be calculated using the formula:
Now, we divide 200 mL by 40 minutes:
The rate of percolation is 5 mL per minute.
Topper's Solved these Questions
Similar Questions
A student conducted an experiment to determine the percolation rate of water in a soil. He observed that it took 45 minutes for 180 mL of water to percolate through the soil. Calculate the percolation rate of water in soil.
View SolutionWater flows through a capillary tube of radius r and length l at a rate of 40 mL per second, when connected to a pressure difference of h cm of water. Another tube of the same length but radius r/2 is conncected in series with this tube and the combination is connected to the same pressure head. Calculate the pressure difference across each tube and the rate of flow of water through the combination.
View Solution
Knowledge Check
Percolation of soil water to water table occurs through
AMicropores less than 0.2μmBMicropores between 0.2 to 20.0 μmCMacropores between 20-50μm.DMacropores bigger than 50 μm.
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal toA0.36 kgB1.2 kgC2.4 kgD3.6 kg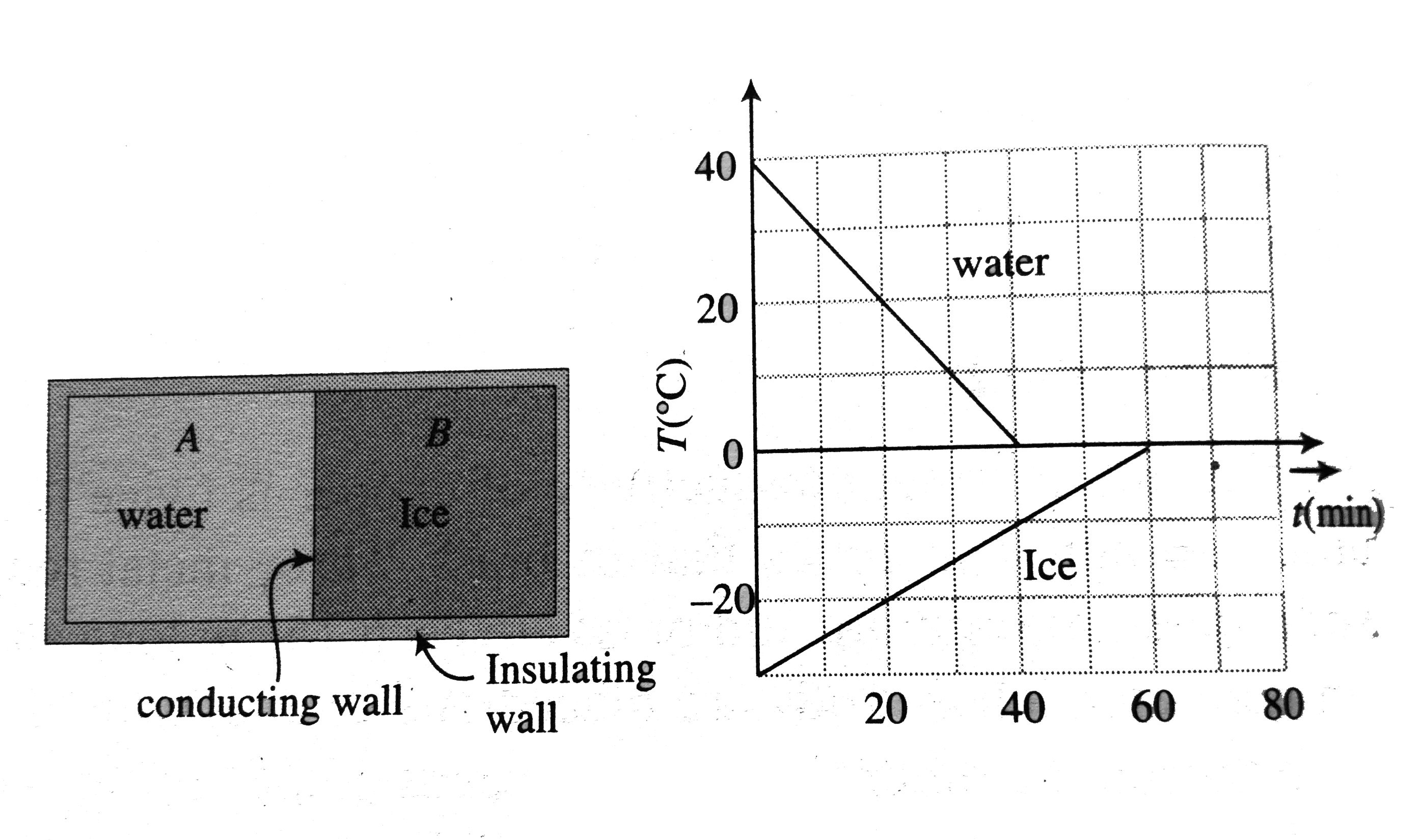
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.AThe value of rate P isB42.0 WC36.0 WD21.0 W
Two vessels A and B of different materials but having identical shape, size and wall-thickness are filled with ice and kep at the same plane. Ice melts at the rate of 100g−1min and 150g−1min in A and B respectively. Assuming that heat enters the vessels through the walls only, calculate the ratio of thermal conductivity of their materials.
View SolutionA pitcher with 1−mm thick porous walls contain 10kg of water. ,Water comes to its outer surface and evaporates at the rate of 0.1gs−1 . The surface area of the pitcher (one side) =200cm2 . The room temperature =42∘C , latent heat of vaporization =2.27×106Jkg−1 , and the thermal conductivity of the porous walls =0.80js−1m−1^(@)C^(-1) . Calculate the temperature of water in the pitcher when it attains a constant value.
View SolutionA flat bottomed metal tank filled with water is dragged along a horizontal floor at the rate of 20m/s The tank is of mass 100 kg and contains 900 kg of water and all the heat produced in the dragging is conducted to the water through the bottom plate of the tank. If the bottom plate has an effective area of conduction 1m2 and thickness 5 cm and the temperature of water in the tank remains constant at 50∘ C, calculate the temperature of the bottom surface of the tank. Given the coefficient of friction between the tank and the floor is 0.5 and K for the material of the tank is 100J/msec K.
View Solution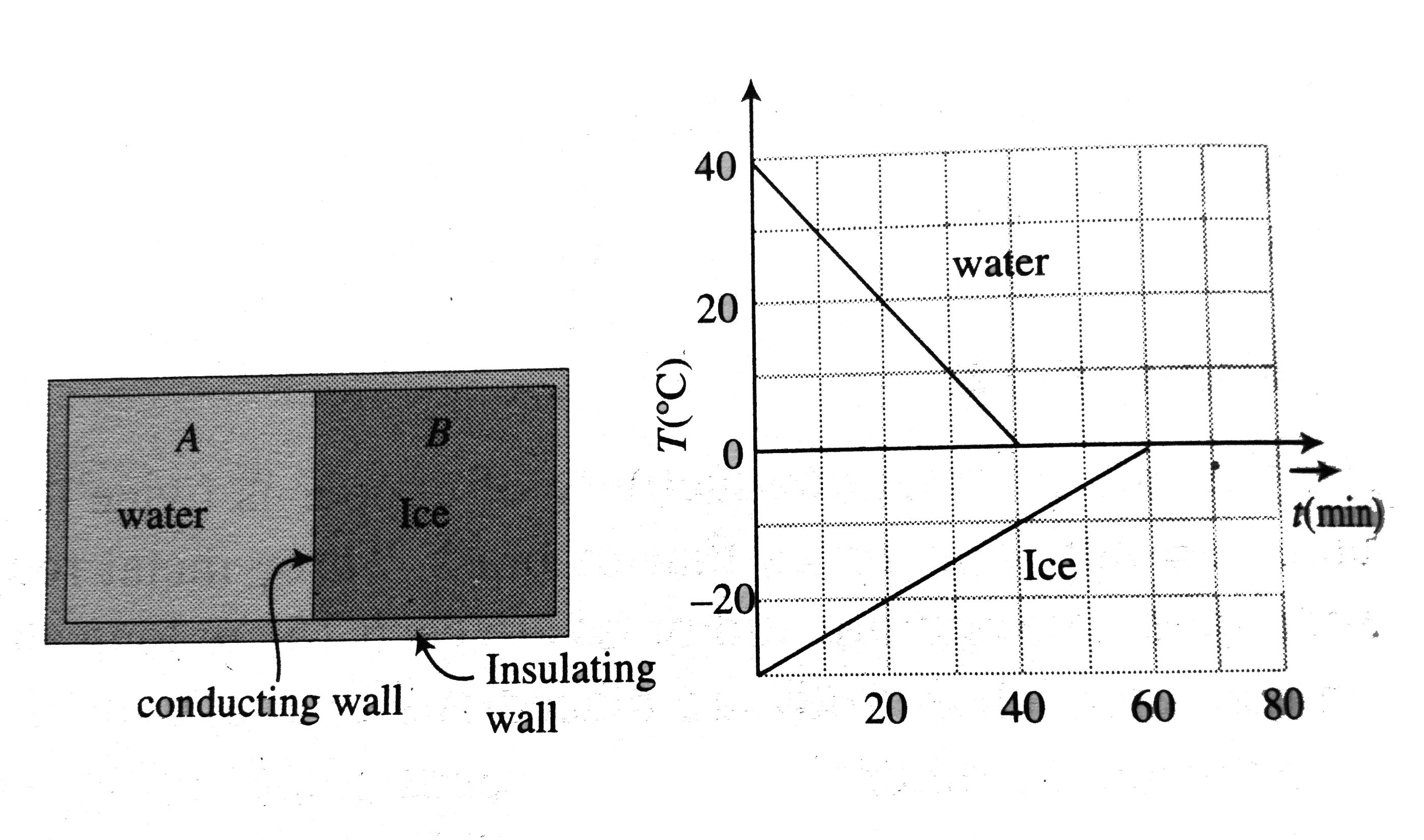
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
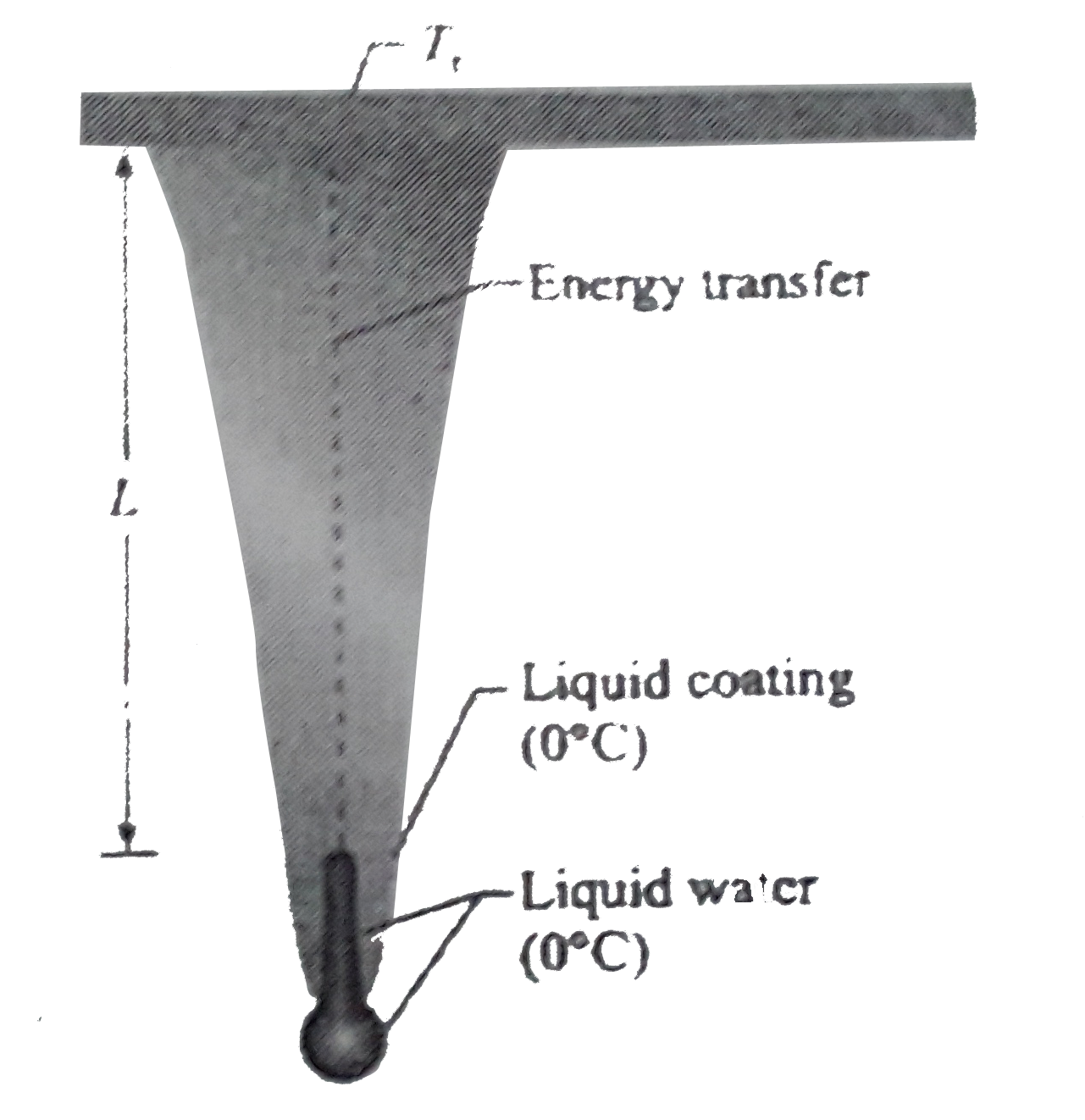
The rate at which the energy conducted upward is
View Solution
