Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wave length associated with the electron revolving around the nucleus.
In order for the electron wave to exist in phase,the circumference of the orbital should be an intergral multiple of the wavelength of the electron wave.otherwise ,the electron wave is out of phase.
mvr=ng/2pi
where mvr=angular momentum
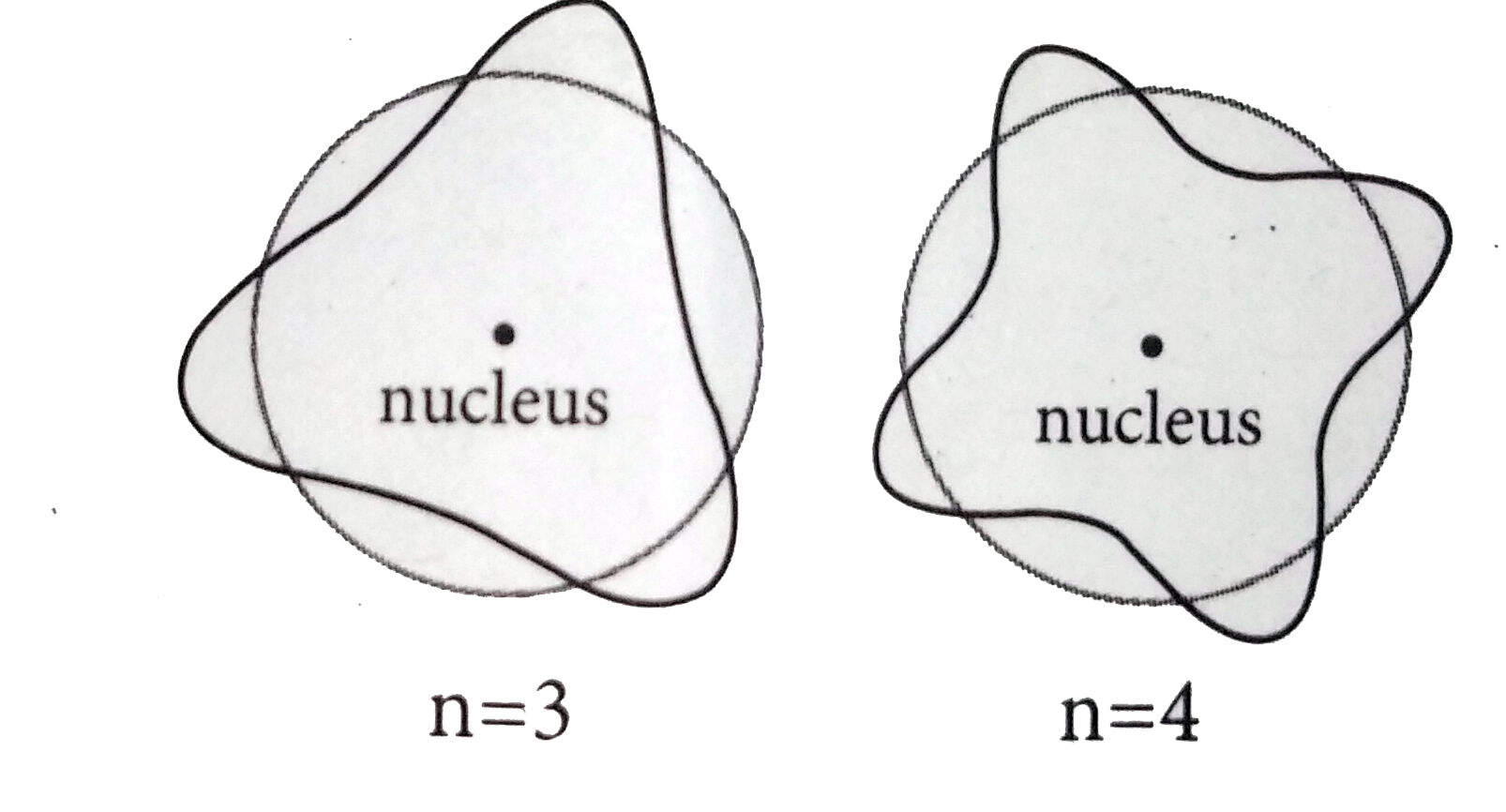 where =circumference of the orbit.
where =circumference of the orbit.
n= 3 , n=4
Topper's Solved these Questions
- QUANTUM MECHANICAL MODEL OF ATOMBOOK - FULL MARKSCHAPTER - QUANTUM MECHANICAL MODEL OF ATOMEXERCISE - IN-TEXT QUESTION-EVALUATE YOURSELF
8 Videos
- QUANTUM MECHANICAL MODEL OF ATOMBOOK - FULL MARKSCHAPTER - QUANTUM MECHANICAL MODEL OF ATOMEXERCISE - ADDITIONAL QUESTIONS SOLVED (choose the Correct Answer)
11 Videos
- QUANTUM MECHANICAL MODEL OF ATOMBOOK - FULL MARKSCHAPTER - QUANTUM MECHANICAL MODEL OF ATOMEXERCISE - Additional Questions Solved (5-Mark Questions)
6 Videos
- PHYSICAL AND CHEMICAL EQUILIBRIUMBOOK - FULL MARKSCHAPTER - PHYSICAL AND CHEMICAL EQUILIBRIUMEXERCISE - ADDITIONAL QUESTIONS SOLVED (NUMERICAL PROBLEMS)
3 Videos
- SAMPLE PAPER - 10 (SOLVED)BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 10 (SOLVED)EXERCISE - PART - IV
10 Videos
Similar Questions
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
View SolutionShow that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
View Solution
Knowledge Check
The De Broglie wavelenght associated with electron in n Bohr orbit is
A2πrnA0B2πnA0C1nA0DnA0The radius of the second orbit of an electron in hydrogen atom is 2.116A. The de Broglie wavelength associated with this electron in this orbit would be
A6.64AB1.058AC2.116AD13.28A
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
View SolutionShow that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
View SolutionThe circumference of circular orbit of electron in a He+ ion is five times the de-Broglie wavelength associated with the electron. Find the radius of the orbit.
View SolutionState the expression for the radius of the nth Bohr orbit in a hydrogen atom. Hence state the expression for the de Broglie wavelength associated with the electron in this orbit.
View SolutionThe radius of the second orbit of an electron in hydrogen atom is 2.116A. The de Broglie wavelength associated with this electron in this orbit would be
View SolutionThe circumference of the second orbit of an atom or ion having single electron is 4 nm the de Broglie wavelength of electron (in nm) revolving in this orbit si :
View Solution
