Show what universal gas constant represents work done per degree per mole ?

Video Solution

Answer

Step by step video & image solution for Show what universal gas constant represents work done per degree per mole ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 CHEMISTRY STATES OF MATTER

Topper's Solved these Questions

STATES OF MATTER : GASES AND LIQUIDSBOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Concept Based Questions
32 Videos
STATES OF MATTER : GASES AND LIQUIDSBOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Additional Important Questions
22 Videos
STATES OF MATTER : GASES AND LIQUIDSBOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - Exercise Fully Solved
23 Videos
STATES OF MATTER (SOLID STATE CHEMISTRY)BOOK - DINESH PUBLICATIONCHAPTER - STATES OF MATTER (SOLID STATE CHEMISTRY)EXERCISE - ULTIMATE PREPARATORY PACKAGE
21 Videos
STRUCTURE OF ATOMBOOK - DINESH PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Reason Type Questions
1 Videos

Knowledge Check

The unit of universal gas constant is
A $watt / K$
B $dyne /^{\circ} C$
C $erg / K$
D $newton /^{\circ} R$
The dimensions of universal gas constant is
A $[M L^{2} T^{- 2} θ^{- 1}]$
B $[M L^{2} T^{- 2} θ]$
C $[M L^{3} T^{- 2} θ^{- 1}]$
DNone of these
One mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:

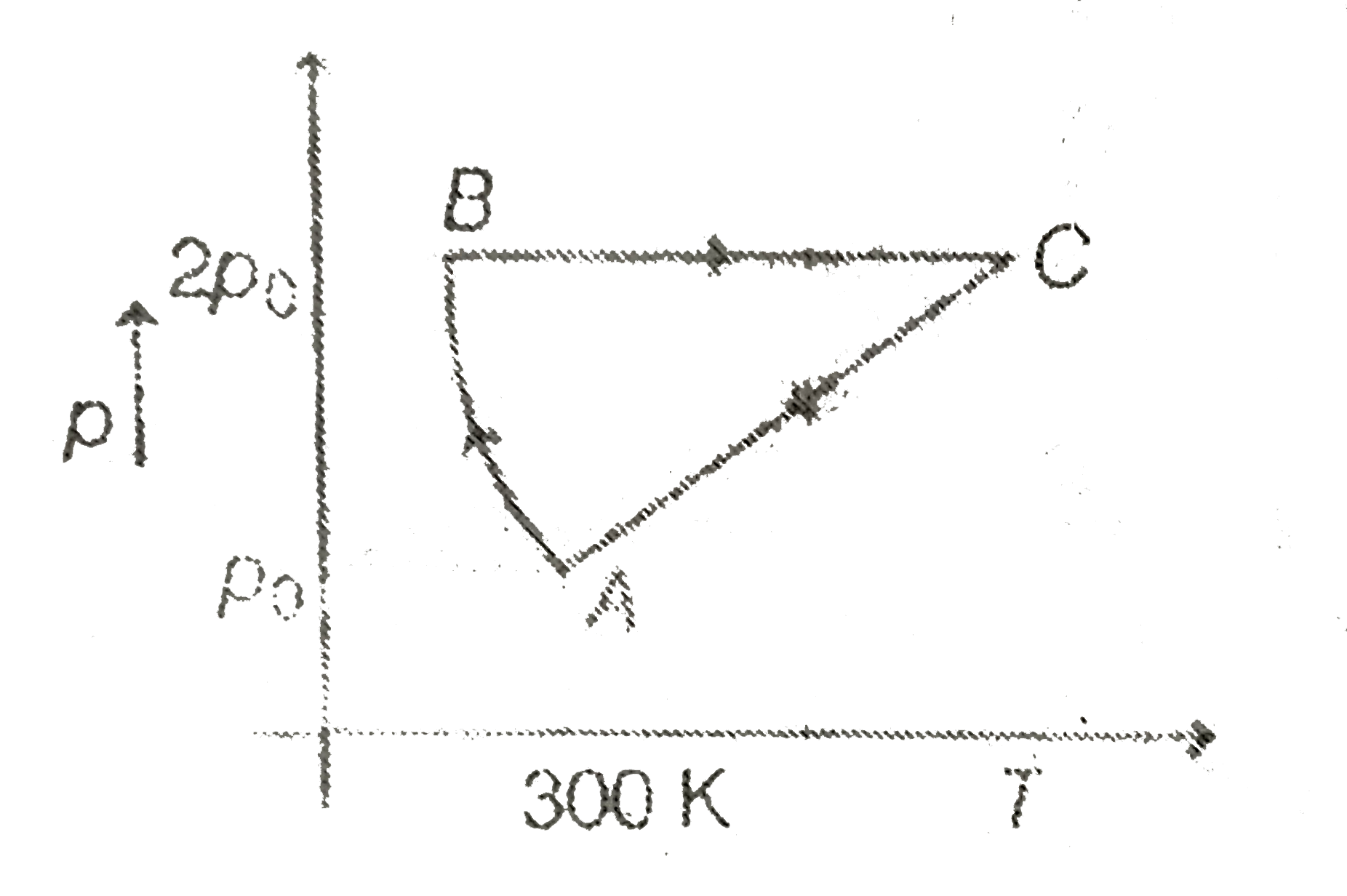
work done on gas in the process AB is
A675 R
B975 R
C300 R
D600 R

DINESH PUBLICATION-STATES OF MATTER : GASES AND LIQUIDS-Short Answer Type Questions

Home
Ask Doubt
Profile

Show what universal gas constant represents work done per degree per mole ?

Topper's Solved these Questions

Similar Questions

Knowledge Check

The unit of universal gas constant is

The dimensions of universal gas constant is

One mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then: work done on gas in the process AB is

DINESH PUBLICATION-STATES OF MATTER : GASES AND LIQUIDS-Short Answer Type Questions

One mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:

work done on gas in the process AB is