The common salt was obtained from two different sources. In one sample, the percentage of chlorine was found to be 60.75 %. In the second sample, 3.888 g of chlorine were present in 6.4 g of the salt. Show that these data are in accordance to the law of constant proportion.
To show that the data from the two samples of common salt are in accordance with the law of constant proportion, we will follow these steps:
Step 1: Understand the Law of Constant Proportion
The law of constant proportion states that a given compound always contains the same elements in the same proportion by mass, regardless of its source. For our case, we need to show that the percentage of chlorine in both samples of salt is the same.
Step 2: Analyze the First Sample
In the first sample, the percentage of chlorine is given as:
- Percentage of Chlorine = 60.75%
Step 3: Analyze the Second Sample
In the second sample, we have:
- Mass of chlorine = 3.888 g
- Mass of salt = 6.4 g
We need to calculate the percentage of chlorine in this sample.
Step 4: Calculate the Percentage of Chlorine in the Second Sample
To find the percentage of chlorine in the second sample, we can use the formula:
Percentage of Chlorine=(Mass of ChlorineMass of Salt)×100
Substituting the values:
Percentage of Chlorine=(3.888g6.4g)×100
Step 5: Perform the Calculation
Calculating the above expression:
Percentage of Chlorine=(3.8886.4)×100≈60.75%
Step 6: Compare the Results
Now we compare the percentage of chlorine from both samples:
- First sample: 60.75%
- Second sample: 60.75%
Since both samples have the same percentage of chlorine, we conclude that the data are in accordance with the law of constant proportion.
Conclusion
Both samples of common salt contain chlorine in the same proportion (60.75%), thus confirming the law of constant proportion.
---
The law of constant proportion states that a given compound always contains the same elements in the same proportion by mass, regardless of its source. For our case, we need to show that the percentage of chlorine in both samples of salt is the same.
In the first sample, the percentage of chlorine is given as:
- Percentage of Chlorine = 60.75%
In the second sample, we have:
- Mass of chlorine = 3.888 g
- Mass of salt = 6.4 g
To find the percentage of chlorine in the second sample, we can use the formula:
Percentage of Chlorine=(Mass of ChlorineMass of Salt)×100
Substituting the values:
Percentage of Chlorine=(3.888g6.4g)×100
Calculating the above expression:
Percentage of Chlorine=(3.8886.4)×100≈60.75%
Now we compare the percentage of chlorine from both samples:
- First sample: 60.75%
- Second sample: 60.75%
Both samples of common salt contain chlorine in the same proportion (60.75%), thus confirming the law of constant proportion.
Topper's Solved these Questions
- SOME BASIC CONCEPTS OF CHEMISTRY BOOK - ICSECHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - REVIEW EXERCISES
129 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY BOOK - ICSECHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
34 Videos
- SELF ASSESSMENT PAPER 2BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 2EXERCISE - Questions
62 Videos
- SOME P-BLOCK ELEMENTS BOOK - ICSECHAPTER - SOME P-BLOCK ELEMENTS EXERCISE - NCERT TEXTBOOK EXERCISES (With Hints and Solutions)
63 Videos
Similar Questions
Copper oxide was prepared by two different methods. In case, 1.75 g of the metal gave 2. 19 g of oxide. In the second case, 1.14 g of the metal gave 1.43 g of the oxide, show that the given data illustrate the law of constant proportions.
View SolutionCopper oxide was prepared by two different methods. In case, 1.75 g of the metal gave 2. 19 g of oxide. In the second case, 1.14 g of the metal gave 1.43 g of the oxide, show that the given data illustrate the law of constant proportions.
View SolutionElement X and Y form two different compounds. In the first compound, 0.324gX is combined with 0.471gY. In the second compound, 0.117gX is combined with 0.509gY. Show that these data illusttate the law of multiple proportions.
View SolutionElement X and Y form two different compounds. In the first compound, 0.324gX is combined with 0.471gY. In the second compound, 0.117gX is combined with 0.509gY. Show that these data illusttate the law of multiple proportions.
View SolutionThis law was proposed by Dalton in 1803 . According to this law , if two elements combune to form more than one compounds ,the masses of one element that combine with a fixed mass of the other element, are in the ratio of small whole number.
For exemple, hydrogen combines with oxygen to form two compounds ,namely, water and hydrogen peroxide.
Here, the masses of oxygen (i.e, 16g and 32g) which combine with a fixed mass of hydrogen (2g) bear a simple raio, i.e, 16 :32 or 1 :2 .
An element forms two oxides .In one oxide ,one gram of the oxide containd 0.5g of the element. In another oxide, 4g of the oxide contains 0.8g of the element . Show that these data confirm the law of multiple proportion.
View SolutionThis law was given by, a French chemist , Joseph Proust. He stated that a given compound always contains exactly the same proportion of elements by weight.
Proust worked with two samples of curpic carbonate- one of which was of natural origin and the other was synthetic one . He found that the composition of elements present in it was for both the samples as shown below:
Thus, irrespective of the source, a given compound always contains same elements in the same proportion. The validity of this law has been confrmed by various experiments. It is sometimes also reffered to as Law of constant composition.
Limitation:
This law is not applicable if the compound is formed from different isotopes of an element . The two isotopes of carbon C-12 and C-14 form carbondioxide C12O2 and C14O2 . The ratio of C : O is 12 : 32 and 14 : 32 respectively .It is not a constant ratio.
0.5 G silver is dissolved in excess of nitric acid. This solution is treated with excess of NaCl solution when 0.66 g AgCl is formed. One gram metallic silver wire is heated in dry Cl2 ,1.32 g AgCl is formed . Show that these data confirm the law of constant proportion.
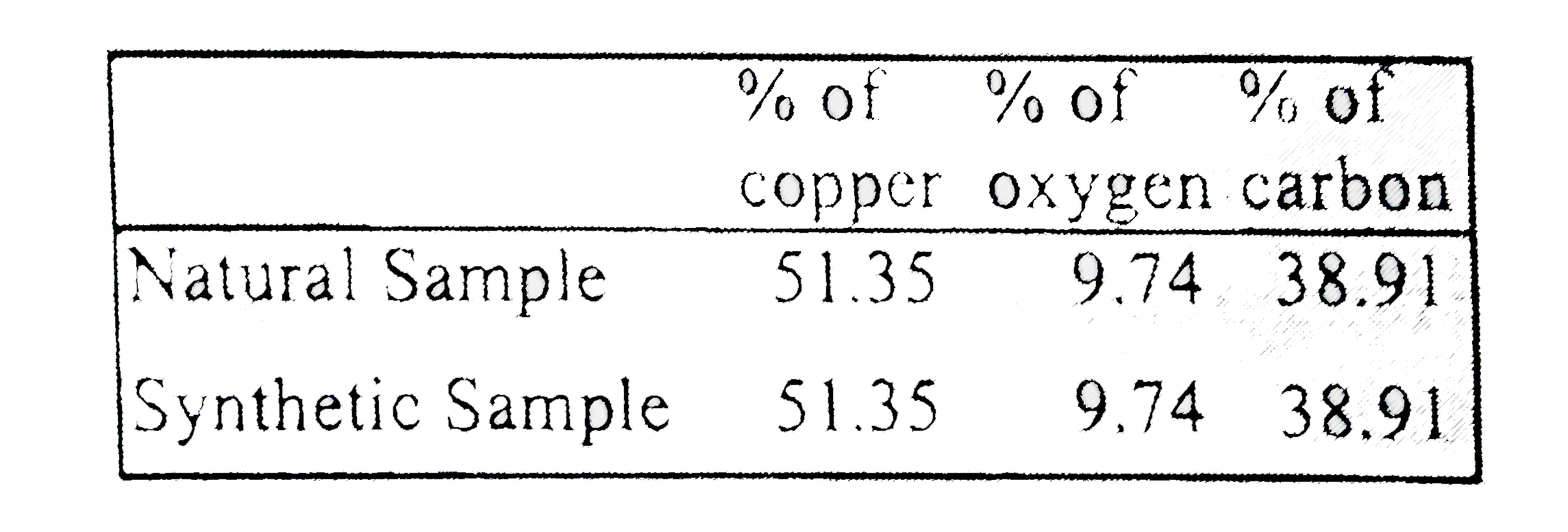
View SolutionHydrogen and oxygen are known to from two compounds. The hydrogen content in one one of these is 5.93% while in the other it is 11.2%. Show that this data illustrates the law of multiple proportions.
View SolutionThis law was proposed by Dalton in 1803 . According to this law , if two elements combune to form more than one compounds ,the masses of one element that combine with a fixed mass of the other element, are in the ratio of small whole number.
For exemple, hydrogen combines with oxygen to form two compounds ,namely, water and hydrogen peroxide.
Here, the masses of oxygen (i.e, 16g and 32g) which combine with a fixed mass of hydrogen (2g) bear a simple raio, i.e, 16 :32 or 1 :2
0.11 g of an oxide of nitrogen gives 56 Ml N2 at 273K and 1 atm. 0.15 g of another oxide of nitrogen gives 56mL N2 at 1 atm , 273K. Show that these data confirm the law of multiple proportion.
View SolutionTwo gaseous samples were analysed. One contained 1.2 g of carbon and 3.2 g of oxygen. The other contained 27.3% carbon and 72.7% oxygen. The experiemental data is an accordance with
View SolutionCommon salt obtained from sea-water contains 8.775%NaCl by mass. The number of formula units of NaCl present in 25g of this salt is :
View Solution
