The decomposition of H2O2, in the presence of Iodide ion has been found to be first order in H2O2 .
The rate constant has been found to be 1.01×10−2−1min. What concentration of H2O2 would give rate of 1.12 xx 10^-2 mol L^-1 min^-1?
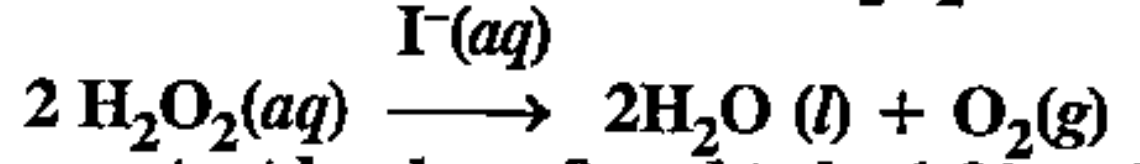 Solution in Punjabi
Solution in Punjabi
2H2O2(aq)1(aq)−−−→2H2O(l)+O2(g)
Rate=k[H2O2]
r=(1.01×10−2−1min)[H2O2]
(∵k=1.01×10−2−1min)
(i) Rate, r=?,[H2O2]=0.4 mol L−1
r=(1.01×10−2 min−1)×(0.4 mol L−1)
=4.04×10−3 mol L−1−1min
(ii) [H2O2]=12×0.4 mol L−1
=0.2 mol L−1
r=(1.01×10−2−1min)×(0.2× mol L−1)
=2.02×10−3 mol L−1−1min
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Numerical Problems63videos
CHEMICAL KINETICS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - BIOMOLECULES EXERCISE - QUESTION BANK85videos
BIOMOLECULES
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - QUESTIONS76videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The rate constant of a reaction is 1.5×107sec−1 at 50∘C and 4.5×107sec−1 at 100∘C. Calculate energy of the activation for the reaction.
01:25View SolutionCovalent compounds are soluble in
02:19View SolutionWhat is a medicine ?
02:16View SolutionThe volume strength of 1 M H_2 O_2 is (molar mass of H_2 O_2 = 34 g "mol"^(-1))
01:58View SolutionThe decomposition of H_2 O_2 , in the presence of Iodide ion has been found to be first order in H_2 O_2 . The rate constant has been found to be 1.01xx10^-2 min^-1 . What concentration of H_2 O_2 would give rate of 1.12 xx 10^-2 mol L^-1 min^-1?
01:22View SolutionDecomposition of H2O2 is accelerated by
01:58View SolutionConsider the following first order reaction. 2H_2 O_2 (aq) overset(I^(-) (aq))to 2H_2 O (l) +O_2 (g) If the rate constant of the reaction is 1.01 xx 10^(-2) min^(-) What concentration of H_2 O_2 would give rate of 1.12 xx 10^(-2) mol L^(-) min^(-) ?
01:22View SolutionConsider the following first order reaction. 2H_2 O_2 (aq) overset(I^(-) (aq))to 2H_2 O (l) +O_2 (g) If the rate constant of the reaction is 1.01 xx 10^(-2) min^(-) Calculate rate of reaction when [H_2 O_2]=0.5 mol L^(-)
01:58View SolutionConsider the following first order reaction.
2H2O2(aq)I−(aq)−−−−→2H2O(l)+O2(g)
If the rate constant of the reaction is 1.01×10−2−min
What concentration of H2O2 would give rate of 1.12×10−2molL−−min?01:22View SolutionConsider the following first order reaction.
2H2O2(aq)I−(aq)−−−−→2H2O(l)+O2(g)
If the rate constant of the reaction is 1.01×10−2−min
Calculate rate of reaction when [H2O2]=0.5molL−02:08View SolutionConsider the following first order reaction.
2H2O2(aq)I−(aq)−−−−→2H2O(l)+O2(g)
If the rate constant of the reaction is 1.01×10−2−min
What concentration of H2O2 would give rate of 1.12×10−2molL−−min?02:08View SolutionConsider the following first order reaction.
2H2O2(aq)I−(aq)−−−−→2H2O(l)+O2(g)
If the rate constant of the reaction is 1.01×10−2−min
Calculate rate of reaction when [H2O2]=0.5molL−04:15View SolutionThe decomposition of hydrogen peroxide in the presence of iodide ion has been found to be first order with respect to H2O2 with rate constant k is 1.01×10−2−1min. Calculate the rate of reaction when
[H2O2]=0.15molL−104:15View SolutionThe decomposition of hydrogen peroxide in the presence of iodide ion has been found to be first order with respect to H2O2 with rate constant k is 1.01×10−2−1min. Calculate the rate of reaction when
[H2O2]=0.15molL−104:15View SolutionThe decomposition of H_2O_2 in the presence of iodide ion has been found to be first order in H_2O_2 . underset((al))(2H_2O_2) overset(I^(-))(rarr)underset((l))(2H_2O) + underset((g))(O_2) The rate constant has been found to be 1.01 xx 10^(-2) "min"^(-1) . Calculate ROR (i) [H_2O_2] = 0.4 mol//L (ii) Concentration of H_2O_2 becomes half.
02:19View SolutionThe decomposition of hydrogen peroxide in the presence of iodide ion has been found to be first order in H2O2:
2H2O2(aq)1−(aq)−−−−→2H2O(l)+O2(g).
The rate constant has been found to be 1.01×10−2 min−1 :
(a) Calculate the rate of reaction when [H2O2]=0.4 mol lit−1.
(b) What concentration of [H2O2] would give a rate of 1.12×10−2 mol lit−1 min−1 ?04:15View Solution

