The following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣
∣
∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣
∣
∣∣
Calculate the rate constant.
To calculate the rate constant for the thermal decomposition of N2O5, we can follow these steps:
Step 1: Write the balanced chemical equation
The balanced equation for the decomposition of N2O5 is:
2N2O5(g)→2N2O4(g)+O2(g)
Step 2: Understand the initial and final conditions
At time t=0:
- Total pressure P0=0.5atm (only N2O5 is present)
At time t=100s:
- Total pressure Pt=0.512atm
Step 3: Relate pressure changes to the extent of reaction
Let x be the change in pressure due to the reaction. The pressure of N2O5 decreases by 2x (since 2 moles decompose), while the pressures of N2O4 and O2 increase by 2x and x respectively.
The total pressure at t=100s can be expressed as:
Pt=P0−2x+2x+x=P0+x
Given Pt=0.512atm and P0=0.5atm, we can set up the equation:
0.512=0.5+x
Step 4: Solve for x
Rearranging gives:
x=0.512−0.5=0.012atm
Step 5: Calculate the pressure of N2O5 at t=100s
The pressure of N2O5 at t=100s is:
PN2O5=P0−2x=0.5−2(0.012)=0.5−0.024=0.476atm
Step 6: Use the first-order rate equation to find the rate constant k
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0Pt)
Substituting the values:
k=2.303100log(0.50.476)
Step 7: Calculate the logarithm
Calculating the logarithm:
log(0.50.476)=log(1.05042)≈0.021
Step 8: Calculate k
Now substituting back into the equation for k:
k=2.303100×0.021≈4.83×10−4s−1
Final Answer:
The rate constant k for the thermal decomposition of N2O5 is approximately:
k≈4.83×10−4s−1
---
The balanced equation for the decomposition of N2O5 is:
2N2O5(g)→2N2O4(g)+O2(g)
At time t=0:
- Total pressure P0=0.5atm (only N2O5 is present)
- Total pressure Pt=0.512atm
Let x be the change in pressure due to the reaction. The pressure of N2O5 decreases by 2x (since 2 moles decompose), while the pressures of N2O4 and O2 increase by 2x and x respectively.
Pt=P0−2x+2x+x=P0+x
Given Pt=0.512atm and P0=0.5atm, we can set up the equation:
0.512=0.5+x
Rearranging gives:
x=0.512−0.5=0.012atm
The pressure of N2O5 at t=100s is:
PN2O5=P0−2x=0.5−2(0.012)=0.5−0.024=0.476atm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0Pt)
Substituting the values:
k=2.303100log(0.50.476)
Calculating the logarithm:
log(0.50.476)=log(1.05042)≈0.021
Now substituting back into the equation for k:
k=2.303100×0.021≈4.83×10−4s−1
The rate constant k for the thermal decomposition of N2O5 is approximately:
k≈4.83×10−4s−1
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercise1videos
CHEMICAL KINETICS
- BOOK - NCERT ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - SOLVED EXAMPLE1videos
CHEMICAL KINETICS
- BOOK - NCERT ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Exercise33videos
BIOMOLECULES
- BOOK - NCERT ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Exercise32videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
Knowledge Check
- Question 1 - Select One
The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?A0.35atms−1B2.235×10−3atms−1C7.8×10−4atms−1D1.55×10−4atms−1
The following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume :
2N2O5(g)→2N2O4(g)+O2(g)

Calculate the rate constant.View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g)→SO2(g)+Cl2(g)

What is the rate of reaction when total pressure of 0.65 atm?View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
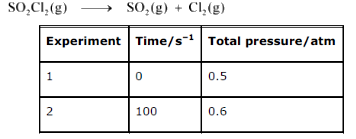
Calculate the rate of the reaction when total pressure is 0.65 atmView SolutionFor the first order reaction
2N2O5(g)→4NO2(g)+O2(g)View SolutionFollowing data were obtained during the thermal decompoistion of sulphuryl chloride at constant volume and 285∘C.
SO2Cl2(g)→SO2+Cl2(g)
∣∣∣Time (s)0240600Pressure (torr)180244302∣∣∣
Show that it is first order reaction.View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant
( given : log 4=0.6021,log2=0.3010)View Solution

