the intial state A has the temperature TAUAas the internal energy of the system . By appling the mechanical work . New state B is achieved with the temperatutre TB and having the interanal energy UB. Given that tB>TA. What is the correct expression for the change in internal energy (ΔV) ?
UB=UA
UB−UA
UA−UB
none of these
The correct Answer is:b
the change in the internal energy is ΔU=UB−UA
Topper's Solved these Questions
- CHEMICAL THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - BITSAT Archives
15 Videos
- CHEMICAL KINETICSBOOK - BITSAT GUIDECHAPTER - CHEMICAL KINETICSEXERCISE - BITSAT Archives
16 Videos
- COORDINATION COMPOUNDSBOOK - BITSAT GUIDECHAPTER - COORDINATION COMPOUNDSEXERCISE - BITSAT Archives
7 Videos
Similar Questions
Statement-1: The internal energy of a system does not change when there is not change in temperature
Statement-2: The internal energy of a gaseous system is state function.
View SolutionThe figure shows two isotherms at temperatures T1 and T2. A gas is taken from one isotherm to another isotherm through different processes. Then change in internal energy ΔU has a relation -
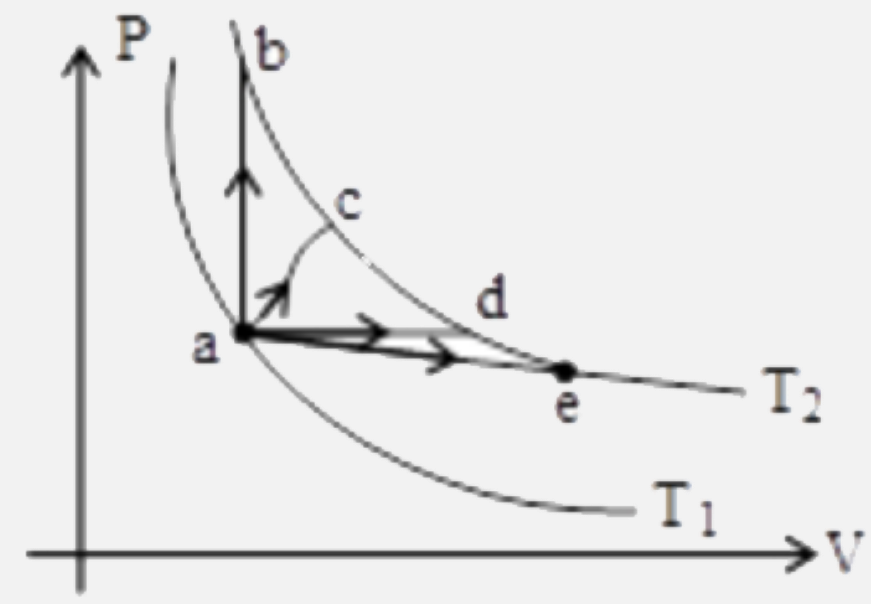
View Solution
Knowledge Check
Statement-1: The internal energy of a system does not change when there is not change in temperature
Statement-2: The internal energy of a gaseous system is state function.AStatement-1 is true, statement-2 is true, statement-2 is a correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is NOT a correct explanation for statement-1CStatement-1 is true, statement-2 is falseDStatement-1 is false, statement-2 is trueA system is changed from state A to state B by one path and from B to A by another path. If ΔE1 and ΔE2 are the corresponding changes in internal energy, then
AE1+E2=−veBE1+E2=+veCE1+E2=0DNone of theseThe internal energy U is a unique function of any state because change in U
Adoes not depend upon pathBdepends upon pathCcorresponds to an adiabatic processDcorresponds to an isothermal process
The figure shows two isotherms at temperatures T1 and T2. A gas is taken from one isotherm to another isotherm through different processes. Then change in internal energy ΔU has a relation -

View SolutionFind total internal energy of 3 moles of hydrogen gas at temperature T.
View SolutionThe internal energy U is a unique function of any state because change in U
View SolutionIn an adiabatic expansion of a gas initial and final temperatures are T1and T2 respectively, then the change in internal energy of the gas is
View SolutionLet ΔU1 and ΔU2 be the changes in internal energy of an ideal gas in the processes A and B then
View Solution
