The n/p ratio for a stable lighter nuclei is about ……………… .
The correct Answer is:One
To solve the question regarding the n/p (neutrons to protons) ratio for stable lighter nuclei, we can follow these steps:
Step 1: Understand the n/p Ratio
The n/p ratio is defined as the ratio of the number of neutrons (n) to the number of protons (p) in a nucleus. This ratio helps us understand the stability of a nucleus.
Step 2: Identify Stable Lighter Nuclei
Stable lighter nuclei typically refer to those with low atomic numbers. Examples include elements like hydrogen, helium, lithium, beryllium, boron, carbon, nitrogen, and oxygen.
Step 3: Calculate n/p Ratio for a Stable Lighter Nucleus
Let's take the example of nitrogen-14 (N-14) to illustrate the calculation:
- Mass Number (A) of nitrogen-14 = 14
- Atomic Number (Z) of nitrogen = 7 (which indicates the number of protons)
Using the formula:
Number of Neutrons (n)=Mass Number (A)−Atomic Number (Z)
n=14−7=7
Now, we can calculate the n/p ratio:
n/p ratio=np=77=1
Step 4: Confirm with Another Example
We can also check another stable lighter nucleus, such as carbon-12 (C-12):
- Mass Number (A) of carbon-12 = 12
- Atomic Number (Z) of carbon = 6
Calculating the number of neutrons:
n=12−6=6
Now, calculating the n/p ratio:
n/p ratio=np=66=1
Conclusion
From the calculations above, we can conclude that the n/p ratio for stable lighter nuclei is approximately 1.
Final Answer
The n/p ratio for a stable lighter nucleus is about 1.
---
The n/p ratio is defined as the ratio of the number of neutrons (n) to the number of protons (p) in a nucleus. This ratio helps us understand the stability of a nucleus.
Stable lighter nuclei typically refer to those with low atomic numbers. Examples include elements like hydrogen, helium, lithium, beryllium, boron, carbon, nitrogen, and oxygen.
Let's take the example of nitrogen-14 (N-14) to illustrate the calculation:
- Mass Number (A) of nitrogen-14 = 14
- Atomic Number (Z) of nitrogen = 7 (which indicates the number of protons)
Number of Neutrons (n)=Mass Number (A)−Atomic Number (Z)
n=14−7=7
n/p ratio=np=77=1
We can also check another stable lighter nucleus, such as carbon-12 (C-12):
- Mass Number (A) of carbon-12 = 12
- Atomic Number (Z) of carbon = 6
n=12−6=6
n/p ratio=np=66=1
From the calculations above, we can conclude that the n/p ratio for stable lighter nuclei is approximately 1.
The n/p ratio for a stable lighter nucleus is about 1.
Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Exercise True/False
20 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Linked Comprehension
3 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Exercises Assertion-Reasoning
14 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
When n/p ratio of an isotope is greater than the stable isotope of that element, it emits
View SolutionIfn/p ratio is high, the nucleus tends to stabilize by :
View SolutionSuppose, the daughter nucleus in a nuclear decay is itself radioactive. Let λpandλd be the decay constants of the parent and the daughter nuclei. Also, let NpandNd be the number of parent and daughter nuclei at time t. Find the condition for which the number of daughter nuclei becomes constant.
View SolutionSuppose, the daughter nucleus in a nuclear decay is itself radioactive. Let λpandλd be the decay constants of the parent and the daughter nuclei. Also, let NpandNd be the number of parent and daughter nuclei at time t. Find the condition for which the number of daughter nuclei becomes constant.
View SolutionSuppose, the daughter nucleus in a nuclear decay is itself radioactive. Let λpandλd be the decay constants of the parent and the daughter nuclei. Also, let NpandNd be the number of parent and daughter nuclei at time t. Find the condition for which the number of daughter nuclei becomes constant.
View SolutionA : Exothermic reactions are possible when two light nuclei fuse or when a heavy nucleus undergoes fission into intermediate mass nuclei.
R: The nature of nuclear binding energy curve is such that it rises lighter nuclei and slightly decreasing for heavier nuclei.
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atmoic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. When n/p ratio is higher than required for stability, the nuclei have the tendency to emit β-rays. while when n/p ratio is lower than required for stability, the nuclei either emits α-particles or a positron or capture K-electron.
For reaction .92M238→.yNx+2.2He4,.yNx→.BLA+2.−1e0
The number of neutrons in the element L is
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atmoic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. When n/p ratio is higher than required for stability, the nuclei have the tendency to emit β-rays. while when n/p ratio is lower than required for stability, the nuclei either emits α-particles or a positron or capture K-electron.
Unstalbe substance exhibit high radioactivity due to
View SolutionTwo radioactive substances have half-lives T and 2T. Initially, they have equal number of nuclei. After time t=4T, the ratio of their number of nuclei is x and the ratio of their activity is y. Then,
View SolutionVarious rules of thumb have seen proposed by the scientific community to expalin the mode of radioactive decay by various radioisotopes. One of the major rules is called the n/p ratio. If all the known isotopes of the elemnts are plotted on a graph of number of neutrons (n) versus number of protons (p), it is observed that all isotopes lying outside of a ''stable'' n/p ratio region are radioactive as shown fig. The graph exhibits straight line behaviour with unit slope up to p=25. Above p=25, tgose isotopes with n/p ratios lying above the stable region usually undergo beta decay. Very heavy isotopes (p>83) are unstable because of their relativley large nuclei and they undergo alpha decay. Gamma ray emission does not involve the release of a particle. It represnts a change in an atom from a higher energy level to a lower energy level.
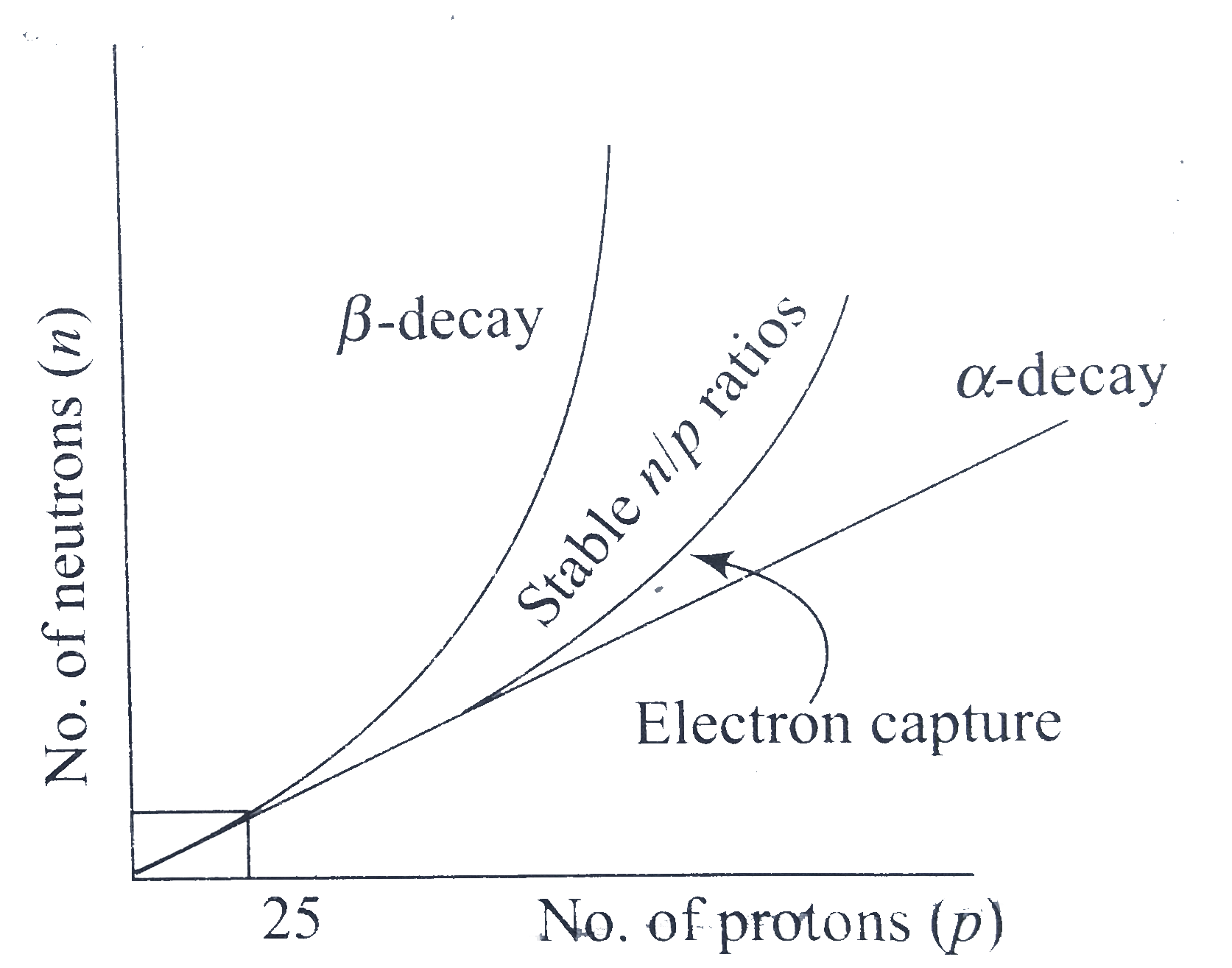
How would the radioisotope of magnesium with atomic mass 27 undergo radioactive decay?.
View Solution
